4.4: Kazi za mstari
- Page ID
- 164673
Kazi ya Linear ni kazi ambayo ina fomu\(f(x) = mx+b\). Mstari wowote ambao unaweza kuonyeshwa kwa fomu pia\(y = mx + b\) ni kazi.
Matumizi kazi nukuu wakati equation ya mstari imeandikwa katika aina Slope-Intercept haina mapungufu au mapumziko na mstari si mstari wima. Kazi ya mstari imeandikwa kama\(f(x) = mx + b\) kupitisha mtihani wa mstari wa wima:
Mtihani wa Mstari wa Wima hutumiwa kuamua kama grafu inafafanua pato la wima kama kazi ya pembejeo ya usawa. Ikiwa mstari wowote wa wima utavuka grafu zaidi ya mara moja, basi grafu haina kufafanua pato moja tu la wima kwa kila pembejeo ya usawa.
Kwa habari zaidi kuhusu equations linear, rejea sehemu ya mistari moja kwa moja.
Unda meza ya ufumbuzi na grafu kazi zifuatazo za mstari:
\(f(x) = 2x − 3\)
Suluhisho
\(f(x) = 2x − 3\)
Ili kupata jozi mbili zilizoamuru, kuchagua maadili madogo ya\(x\), kisha compute maadili ya\(f(x)\).
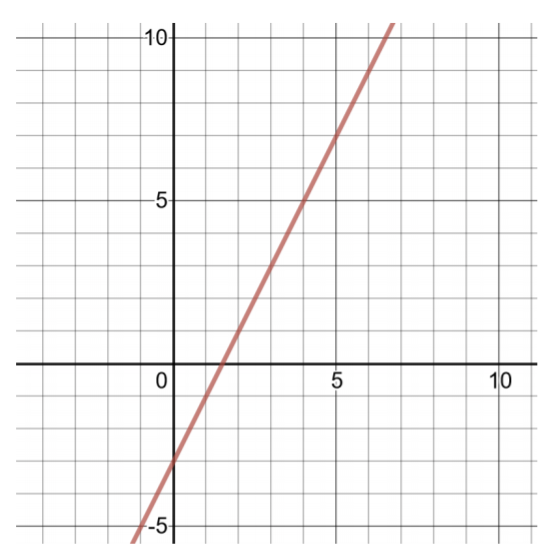
| Jedwali la Solutions kwa\(f(x) = 2x − 3\) | |
| \(x\) | \(f(x)\) |
| -1 | \(f(−1) = 2(−1) − 3 = −2 − 3 = −5\) |
| 0 | \(f(0) = 2(0) − 3 = 0 − 3 = 3\) |
Unda meza ya ufumbuzi na grafu kazi inayofuata ya mstari:
\(g(x) = \dfrac{1}{ 3} x + 4\)
Suluhisho
Ili kupata jozi mbili zilizoamuru, chagua maadili madogo ya x, kisha compute maadili ya\(g(x)\). Kwa sababu mgawo wa neno zenye x ni sehemu, chagua wingi wa denominator kwa bidhaa ya\(\dfrac{1 }{3} x\) kuwa integer.
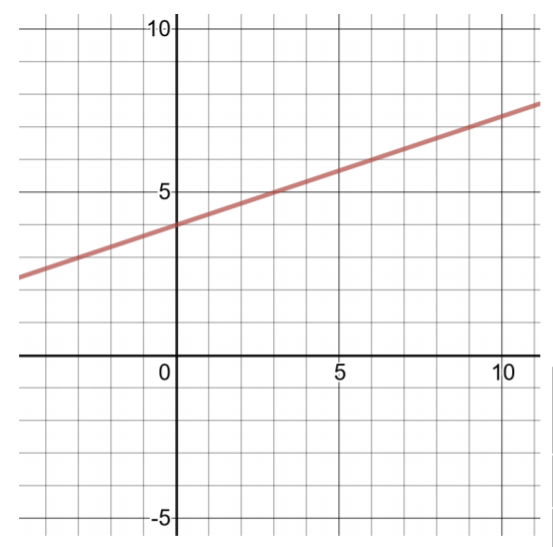
| Jedwali la Solutions kwa\(g(x) =\dfrac{ 1 }{3} x + 4\) | |
| \(x\) | \(g(x)\) |
| 0 | \(g(0) = \dfrac{1 }{3} (0) + 4 = 4\) |
| 3 | \(g(3) = \dfrac{1 }{3} (3) + 4 = 1 + 4 = 5\) |
Unda meza ya ufumbuzi na grafu kazi zifuatazo za mstari:
\(h(x) = −4x − 1\)
Suluhisho
Ili kupata jozi mbili zilizoamuru, kuchagua maadili madogo ya\(x\), kisha compute maadili ya\(h(x)\).
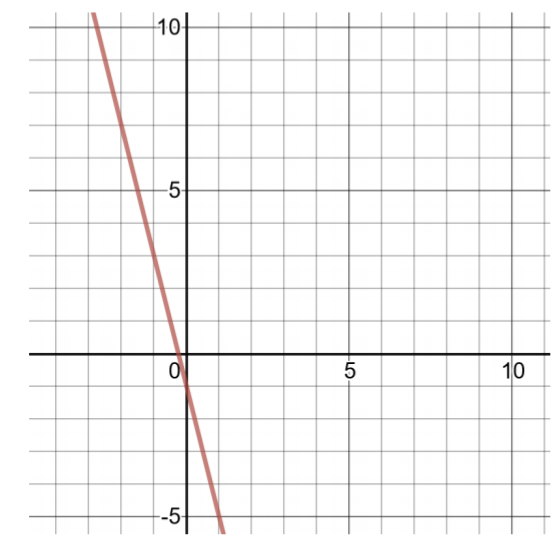
| Jedwali la Solutions kwa\(h(x) = −4x − 1\) | |
| \(x\) | \(h(x)\) |
| 0 | \(h(0) = −4(0) − 1 = −1\) |
| 1 | \(h(1) = −4(1) − 1 = −5\) |
Unda meza ya ufumbuzi na grafu kazi zifuatazo za mstari:
\(h(x) = − \dfrac{3 }{4} x − \dfrac{1 }{4}\)
Suluhisho
Ili kupata jozi mbili zilizoamriwa\(x\), chagua maadili madogo ya, kisha compute maadili\(h(x)\) ya.Kwa sababu mgawo wa neno zenye\(x\) ni sehemu, chagua wingi wa denominator kwa bidhaa ya\(− \dfrac{3}{4} x\) kuwa integer.
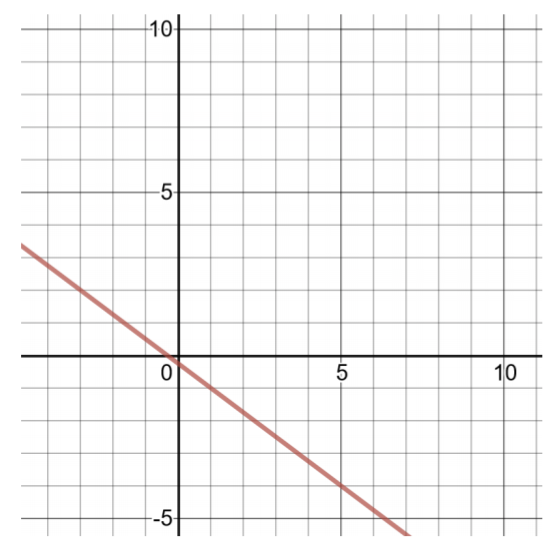
| Jedwali la Solutions kwa\(h(x) = − \dfrac{3}{4} x − \dfrac{1}{4}\) | |
| \(x\) | \(h(x)\) |
| 0 | \(h(0) = − \dfrac{3}{4} (0) − \dfrac{1}{4} = − \dfrac{1}{4}\) |
| 4 | \(h(4) = − \dfrac{3}{4} (4) − \dfrac{1}{4} = −3 − \dfrac{1}{4} = −3 \dfrac{1}{4}\) |
Unda meza ya ufumbuzi na grafu kazi zifuatazo za mstari:
- \(f(x) = 4x − 9\)
- \(g(x) = \dfrac{1}{ 2} x − 2\)
- \(h(x) = −3x + 5\)
- \(f(x) = − \dfrac{2}{ 3} x −\dfrac{ 1 }{3}\)


