2.1: Ufafanuzi na Lebo Quadrants
- Page ID
- 164635
Mfumo wa Kuratibu wa mstatili pia unajulikana kama Mfumo wa Kuratibu wa Cartesian, unategemea gridi ya taifa na hutengenezwa na mistari miwili ya namba ya perpendicular, mstari wa namba ya usawa unaoitwa x-axis na mstari wa namba wima unaoitwa y-axis. Kila hatua kwenye mfumo wa kuratibu mstatili inaweza kutambuliwa na kuratibu za kipekee za x na y.
Mistari miwili ya namba ya perpendicular inakabiliana\((0, 0)\) na hatua na inaitwa asili. Mfumo wa kuratibu mstatili umegawanywa katika mikoa minne. Mikoa huitwa quadrants na iliyoandikwa kwa namba za Kirumi kama ifuatavyo: Quadrant I, Quadrant II, Quadrant III, na Quadrant IV, kama inavyoonekana katika takwimu hapa chini
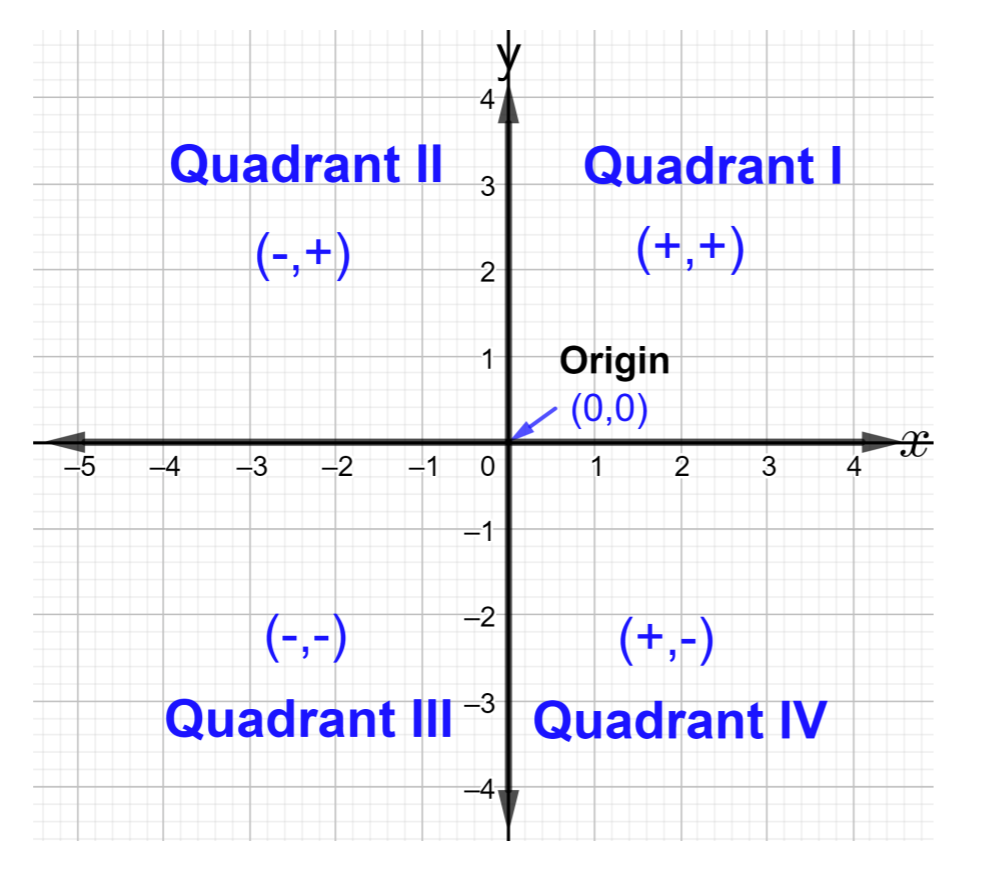
Kila hatua katika ndege ya kuratibu inalingana na jozi ya kipekee iliyoamuru\((x, y)\), wapi\(x\) na\(y\) ni namba yoyote halisi. Jozi zilizoamriwa daima zina kuratibu x-kwanza (upande wa kushoto) na\(y\) -kuratibu pili (upande wa kulia). \((6, 4)\),\(\left(−.33, \dfrac{1}{5} \right)\)\((100, −2)\),\(\left( \sqrt{ 3}, \dfrac{1 }{2}\right )\) ni mifano michache ya jozi zilizoamriwa. Soma jozi kuamuru\((6, 4)\) kama” uhakika sita, nne” ambapo 6 ni\(x\) -kuratibu na 4 ni\(y\) -kuratibu.
- Je! Ni pointi gani zinazoitwa kuwa ni za fomu\((x, y)\)?
- Tambua kuratibu za jozi zifuatazo zilizoamriwa:\((−10, 0)\),\((0.5, −6)\),\(\left(\dfrac{1}{ 2} , −\dfrac{ 5 }{3} \right)\)
- Jina na ueleze jozi iliyoamriwa ya uhakika ambapo pembe za perpendicular za mfumo wa kuratibu mstatili huingiliana.
- Weka mikoa 4 katika mfumo wa kuratibu mstatili.
- Jina la kuratibu kwanza katika jozi iliyoamriwa.
- Jina la kuratibu pili katika jozi iliyoamriwa.
- Nini mstari wa nambari ya usawa katika mfumo wa kuratibu mstatili?
- Nini mstari wa nambari ya wima katika mfumo wa kuratibu mstatili?


