2.2 : Paires commandées
- Page ID
- 165745
Les paires ordonnées sont des paires de nombres utilisés pour localiser un point dans le plan de coordonnées rectangulaires et écrits sous la forme\((x, y)\), où x est la coordonnée x et y est la coordonnée y.
L'emplacement de la paire ordonnée dans les quadrants déterminera le signe des coordonnées x et y, comme indiqué dans la section précédente, figure ci-dessus. Ainsi, les signes des paires ordonnées\((x, y)\) sont résumés comme suit,
- Si\((x, y)\) se trouve dans le quadrant I, alors x et y sont tous deux positifs.
- Si\((x, y)\) se trouve dans le quadrant II, alors x est négatif et y est positif.
- Si\((x, y)\) se trouve dans le quadrant III, alors x et y sont tous deux négatifs.
- Si\((x, y)\) se trouve dans le quadrant IV alors x est positif et y est négatif.
Remarque : Les points situés sur l'axe perpendiculaire dans un plan rectangulaire n'appartiennent à aucun des quadrants.
Pour localiser un point dans le plan de coordonnées, utilisez un processus appelé représentation graphique d'un point. Ce processus peut également être appelé traçage d'un point. Commencez toujours par l'origine et déplacez-vous vers la droite ou la gauche pour localiser la coordonnée X et déplacez-vous vers le haut ou vers le bas pour localiser la coordonnée Y.
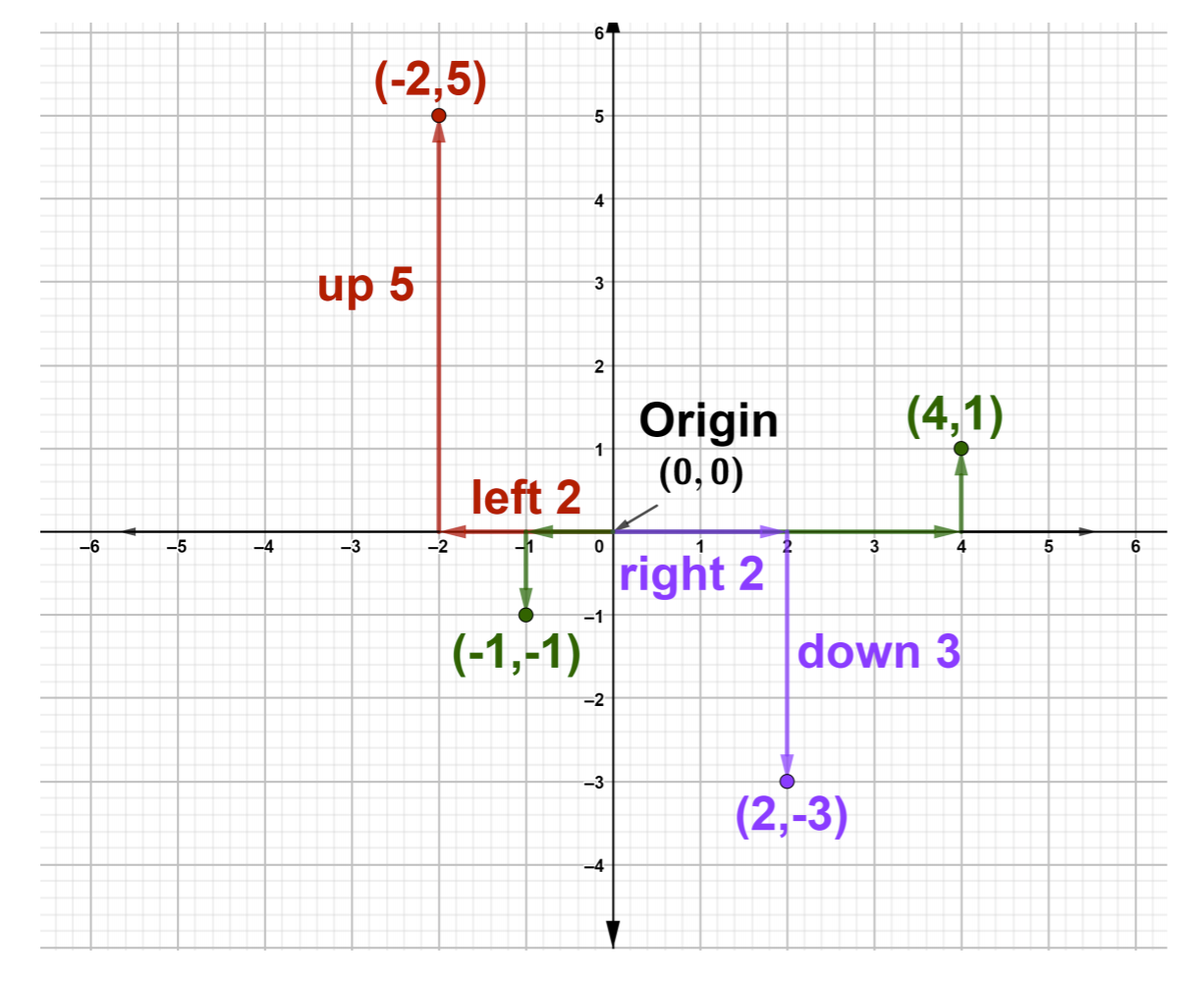
Pour représenter graphiquement ou tracer\((−2, 5)\) sur un plan de coordonnées, commencez par l'origine et déplacez 2 unités vers la gauche, car la coordonnée x −2 est négative, puis déplacez-vous de 5 unités vers le haut car la coordonnée y 5 est positive et tracez un point. Remarquez que notre point se trouve dans le quadrant II. Pour tracer le point\((4, 1)\), commencez par l'origine et déplacez-vous de 4 unités vers la droite et d'une unité vers le haut. De même, tracez les points\((−1, −1)\) et\((2, −3)\), comme le montre la figure ci-dessous.
Fais attention ! Dans le chapitre précédent, la notation\((p, q)\) a été utilisée pour représenter une solution d'inégalité des valeurs absolues en notation par intervalles. Cette section présente des paires ordonnées qui utilisent la même représentation entre parenthèses. Veillez à ne pas confondre la notation par intervalles avec la notation par paires ordonnées.
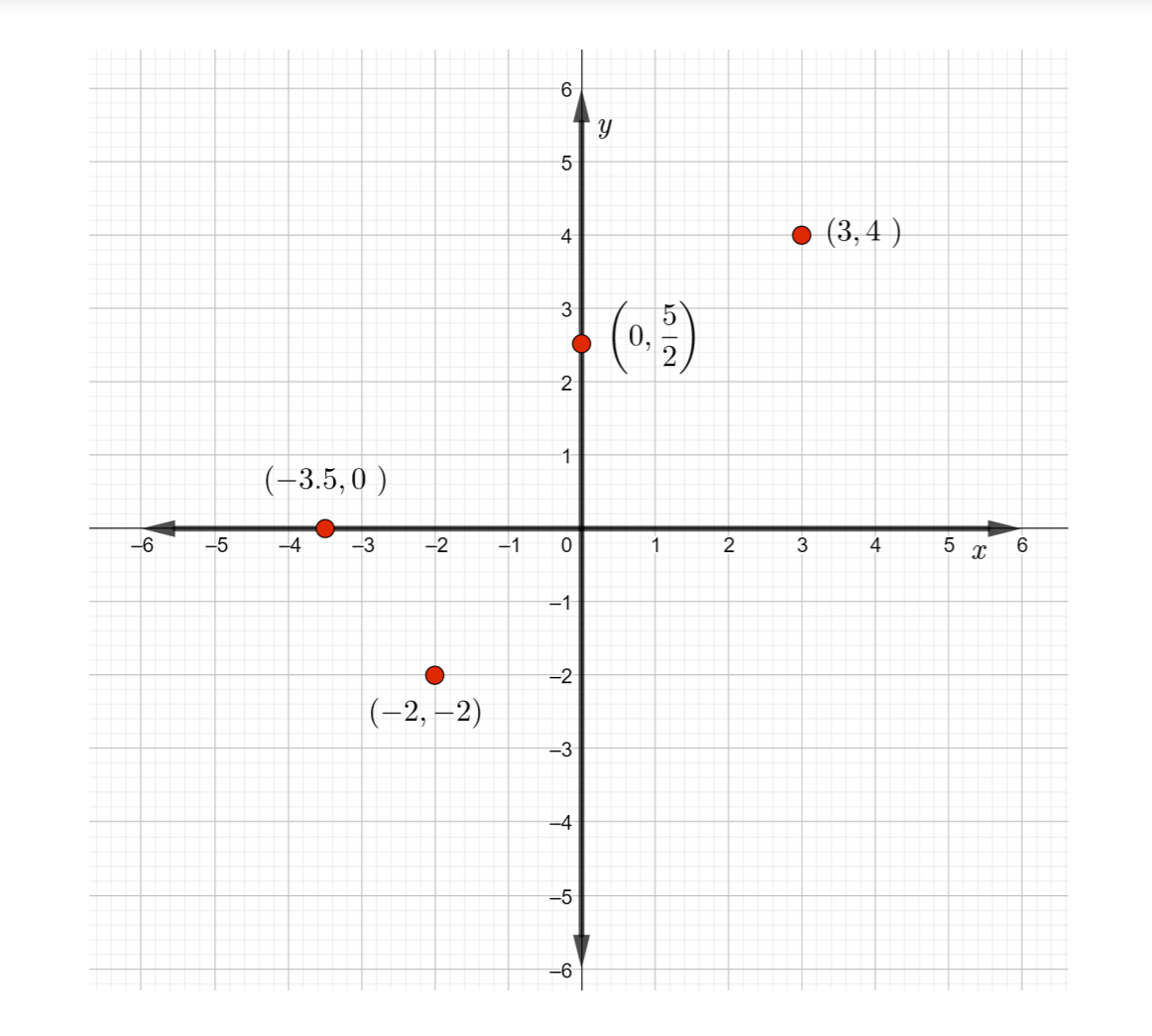
Tracez les points donnés sur le même plan de coordonnées rectangulaires et indiquez où se trouve chaque point. Si un point ne se trouve dans aucun des quadrants, indiquez l'axe sur lequel il se trouve.
- \((3, 4)\)
- \((−2, −2)\)
- \(\left(0, \dfrac{5 }{2 }\right)\)
- \((−3.5, 0)\)
Solution
- Les coordonnées x et y sont positives. Commencez par l'origine, déplacez 3 unités vers la droite puis, remontez de 4 unités et marquez le point.\((3, 4)\) Le point se trouve dans le quadrant I
- Les coordonnées x et y sont négatives. Commencez par l'origine, déplacez 2 unités vers la gauche, puis déplacez 2 unités vers le bas et marquez le point\((−2, −2)\). Le point se trouve dans le quadrant II.
- Comme la coordonnée X est 0, commencez par l'origine et ne vous déplacez pas vers la droite ou la gauche. Puisque la coordonnée y est positive, déplacez les\(\dfrac{5 }{2}\) unités ou 2,5 unités vers le haut. Point d'étiquette\(\left(0, \dfrac{5 }{2} \right)\). Le point se trouve sur l'axe Y.
- Puisque la coordonnée X est négative, commencez par l'origine et déplacez-vous de 3,5 unités vers la gauche. Puisque la coordonnée y est 0, ne vous déplacez pas vers le haut ou vers le bas. Étiquetez le point\((−3.5, 0)\). Le point se trouve sur l'axe des abscisses.
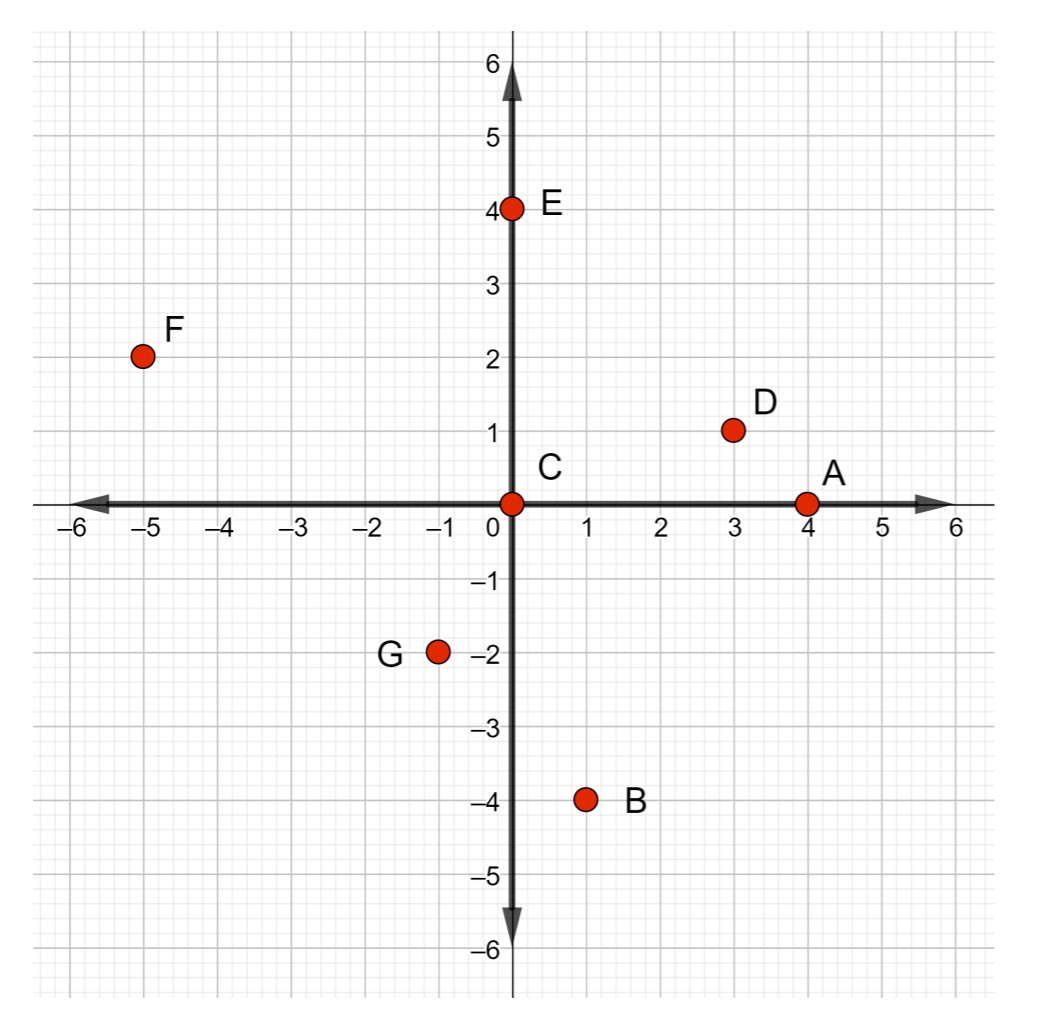
Déterminez les coordonnées des points indiqués dans la figure ci-dessous.
Solution
Pour tracer n'importe quel point dans le plan de coordonnées, commencez par l'origine puis déplacez-vous selon le signe des coordonnées données comme suit,
- Point A : Commencez par l'origine et déplacez 4 unités vers la droite. La coordonnée X est 4. Il n'y a aucun mouvement vertical vers le haut ou vers le bas, donc la coordonnée y est 0. Par conséquent, le point A a des coordonnées\((4, 0)\)
- Point B : Encore une fois, commencez par l'origine et déplacez 1 unité vers la droite et 4 unités vers le bas. Par conséquent, les points B ont des coordonnées\((1, −4)\)
- Point C : Puisque la coordonnée X est 0, commencez par l'origine et ne vous déplacez pas vers la droite ou la gauche. La coordonnée y est également égale à 0, donc ne vous déplacez ni vers le haut ni vers le bas. Ainsi, les coordonnées du point C sont\((0, 0)\)
- Point D : Depuis l'origine, déplacez 3 unités vers la droite, puis 1 unité vers le haut. Ainsi, les coordonnées du point D sont\((3, 1)\)
- Point E : commencez par l'origine et restez-y car la coordonnée X est 0, puis déplacez 4 unités vers le haut. Ainsi, les points E ont des coordonnées\((0, 4)\).
- Point F : Déplace 5 unités à gauche de l'origine et 2 unités vers le haut. Les points F ont des coordonnées\((−5, 2)\)
- Point G : déplace 1 unité vers la gauche de l'origine et 2 unités vers le bas. Les points G ont des coordonnées\((−1, −2)\)
- Quelles sont les coordonnées x et y dans\((−3, 2)\) et\((2, −3)\) ? Sont-ils le même point ?
- Tracez les points suivants sur le même plan de coordonnées rectangulaires et indiquez le quadrant dans lequel se trouve chaque point ou l'axe sur lequel il se trouve. \((−1.5, 2),\quad (0, −3), \quad(5, 2.5),\quad \left(− \dfrac{1}{ 2 },\quad − \dfrac{1 }{2}\right), \quad\left(3\dfrac{1 }{2} ,\quad −\dfrac{ 7 }{2}\right ), \quad (−3, 3),\quad (−2, 0)\)
- Déterminez les coordonnées de chaque point donné dans la figure ci-dessous.
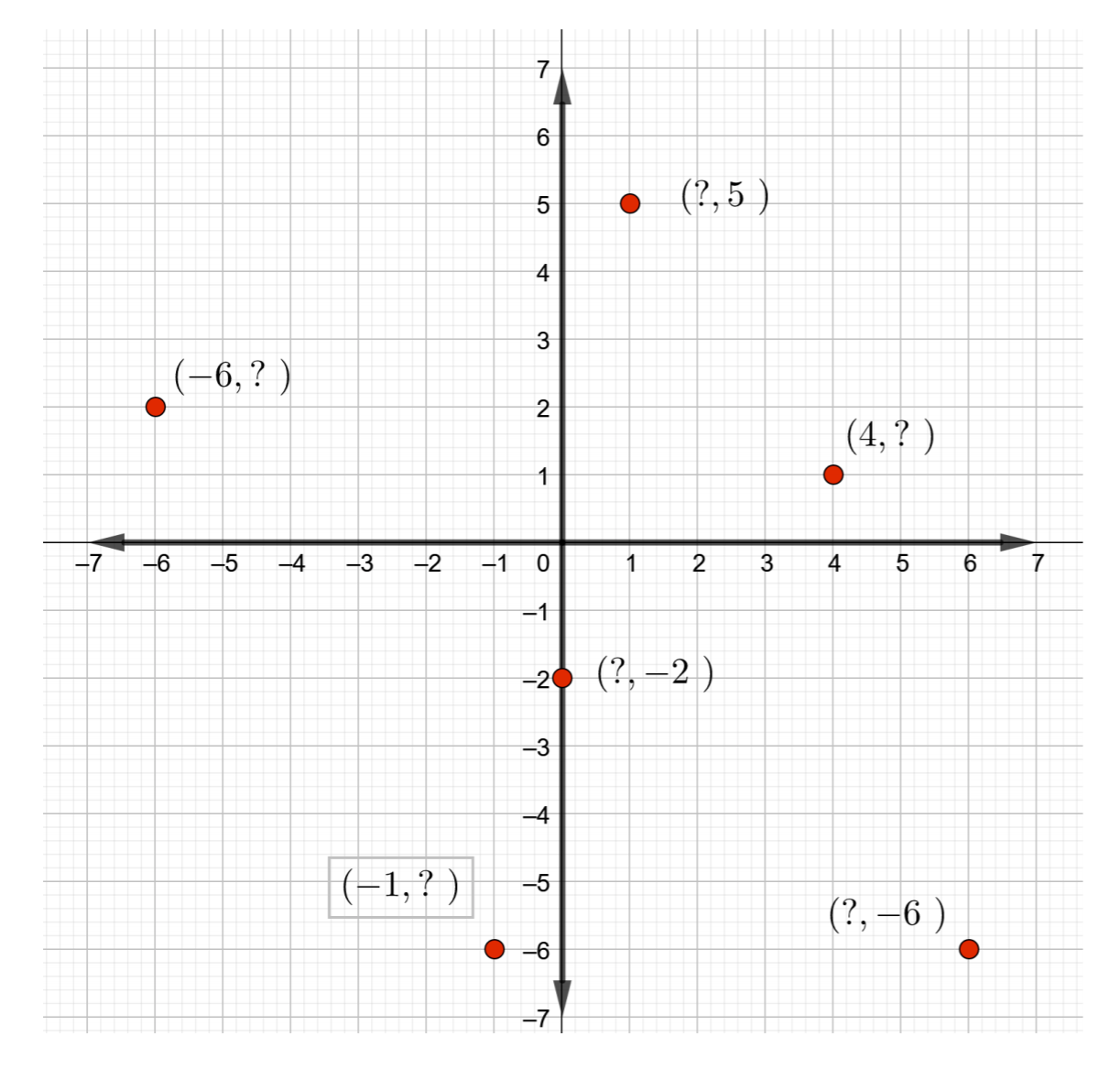
Figure Template:Index - Déterminez les coordonnées de chaque point donné dans la figure ci-dessous.
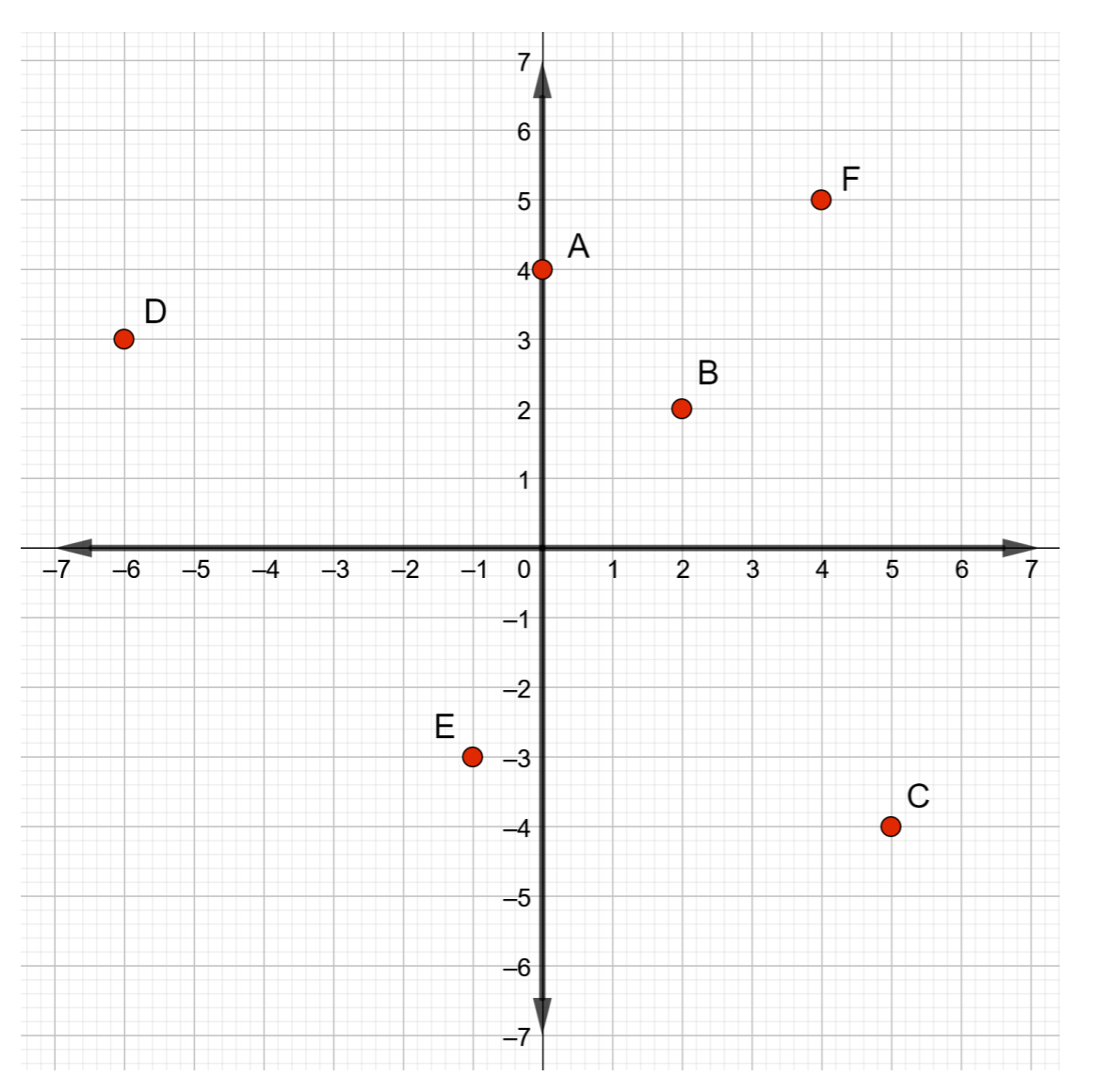
Figure Template:Index


