Home
Français
Chimie 1e (OpenStax)
19 : Métaux de transition et chimie de coordination
19.E : Métaux de transition et chimie de coordination (exercices)

19.E : Métaux de transition et chimie de coordination (exercices)

Last updated
Save as PDF

Page ID: 194003

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

19.1 : Présence, préparation et propriétés des métaux de transition et de leurs composés

Q19.1.1

Écrivez les configurations électroniques pour chacun des éléments suivants :

ARTICLE 19.1.1

La configuration électronique d'un atome est la représentation de la disposition des électrons répartis entre les couches et sous-couches orbitales. La configuration électronique de chaque élément est propre à sa position sur le tableau périodique où le niveau d'énergie est déterminé par la période et le nombre d'électrons est donné par le numéro atomique de l'élément. Il existe quatre types d'orbitales (s, p, d et f) qui ont des formes différentes et chaque orbitale peut contenir un maximum de 2 électrons, mais les orbitales p, d et f ont des sous-niveaux différents, ce qui signifie qu'elles peuvent contenir plus d'électrons.

Le tableau périodique est divisé en groupes que nous pouvons utiliser pour déterminer les orbitales et ainsi écrire des configurations électroniques :

Groupes 1 et 2 : S orbital

Groupes 13 à 18 : P orbital

Groupes 3 à 12 : Orbital D

Lanthanides et actinides : F orbital

Chaque orbitale (s, p, d, f) possède un nombre maximum d'électrons qu'elle peut contenir. Un moyen facile de se souvenir du maximum d'électrons de chaque groupe est de consulter le tableau périodique et de compter le nombre de périodes dans chaque collection de groupes.

Groupes 1 et 2 : 2 (2 électrons au total = 1 orbitale x maximum de 2 électrons = 2 électrons)

Groupe 13 - 18 : 6 (6 électrons au total = 3 orbitales x 2 électrons max = 6 électrons)

Groupe 3 - 12 : 10 (10 électrons au total = 5 orbitales x 2 électrons max = 10 électrons)

Lanthanides et actinides : 14 (14 électrons au total = 7 orbitales x 2 électrons max. = 14 électrons)

Electron remplit les orbitales selon un schéma spécifique qui affecte l'ordre dans lequel les versions à main longue sont écrites :

Schéma de remplissage d'électrons : 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f

Un moyen plus simple et plus rapide d'écrire des configurations d'électrons consiste à utiliser des configurations de gaz rares comme raccourcis. Nous sommes en mesure de le faire parce que les configurations électroniques des gaz rares ont toujours toutes des orbitales remplies.

Lui : 1s ² 2s ²

Nouveau : 1 x ^{2 x 2} x ^{2 x 2} x ⁶

Art : 1s ² 2s ² 2p ⁶ 3s ² 3p ⁶

Kr : 1s ² 2s ² 2p ⁶ 3p ² 3p ⁶ 4s ² 3d ¹⁰ 4p ⁶

Xe : 1s ² 2s ² 2p ⁶ 3s ² 3p ⁶ 4s ² 3d ¹⁰ 4p ⁶ 5s ² 4d ¹⁰ 5p ⁶

Run : 1s ² 2s ² 2p ⁶ 3s ² 3p ⁶ 4s ² 3d ¹⁰ 4p ⁶ 5s ² 4d ¹⁰ 5p ⁶ 6s ² 4f ¹⁴ 5d ¹⁰ 6p ⁶

La configuration de gaz noble la plus couramment utilisée est Ar. Lorsque vous souhaitez utiliser le raccourci de configuration des gaz rares, vous devez placer le symbole du gaz noble entre crochets :

[Art]

puis écrivez-le avant le reste de la configuration, c'est-à-dire uniquement les orbitales qui suivent celle du gaz noble.

a. Sc

Commençons par déterminer où se situe Scandium dans le tableau périodique : ligne 4, groupe 3. Cette identification est la base critique dont nous avons besoin pour écrire sa configuration électronique.

En examinant le numéro atomique du Scandium, 21, il nous donne à la fois le nombre de protons et le nombre d'électrons. À la fin de l'écriture de sa configuration électronique, les électrons devraient totaliser 21.

À la ligne 4, le groupe 3 Sc se trouve un métal de transition, ce qui signifie que sa configuration électronique inclura l'orbitale D.

Maintenant, nous pouvons commencer à assigner les 21 électrons de Sc à des orbitales. Lorsque vous assignez des électrons à leurs orbitales, vous vous déplacez directement dans le tableau périodique.

Ses 2 premiers électrons se trouvent sur l'orbitale 1s, qui est désignée comme

1s ²

où le « 1 » qui précède le s indique qu'il appartient à la première ligne et qu'il a un exposant de 2 parce qu'il atteint le nombre maximal d'électrons de l'orbitale s. Nous avons maintenant 21-2=19 électrons supplémentaires à attribuer.

Ses 2 électrons suivants se trouvent sur l'orbitale 2s, qui est désignée comme

2 x ²

où le « 2 » qui précède le s indique qu'il appartient à la deuxième ligne et qu'il a un exposant de 2 parce qu'il atteint le nombre maximal d'électrons de l'orbitale s. Nous avons maintenant 19-2=17 électrons supplémentaires à attribuer.

Ses 6 électrons suivants se trouvent sur l'orbitale 2p, qui est désignée comme

2 p. ⁶

où le « 2 » qui précède le p indique qu'il appartient à la deuxième ligne et qu'il a un exposant de 6 car il atteint le nombre d'électrons maximal de l'orbitale p. Nous avons maintenant 17 à 6 = 11 électrons supplémentaires à attribuer.

Ses 2 électrons suivants se trouvent sur l'orbitale des 3 s, qui est désignée comme

3 x ²

où le « 3 » qui précède le s indique qu'il appartient à la troisième ligne et qu'il a un exposant de 2 car il atteint le nombre maximal d'électrons de l'orbitale s. Nous avons maintenant 11 à 2 = 9 électrons supplémentaires à attribuer.

Ses 6 électrons suivants se trouvent sur l'orbitale 3p, qui est désignée comme

3 p. ⁶

où le « 3 » qui précède le p indique qu'il appartient à la troisième ligne et qu'il a un exposant de 6 car il correspond au nombre d'électrons maximal de l'orbitale p. Nous avons maintenant 9 à 6 = 3 électrons supplémentaires à attribuer.

Ses 2 électrons suivants se trouvent sur l'orbitale 4s, qui est désignée comme

4 x ²

où le « 4 » qui précède le s indique qu'il appartient à la ligne quatre et qu'il a un exposant de 2 car il atteint le nombre maximal d'électrons de l'orbitale s. Nous avons maintenant 3 à 2 = 1 électron de plus à attribuer.

Son dernier électron serait seul sur l'orbitale 3D, désignée comme

3d ¹

où le « 3 » précédant le d indique que, même s'il s'agit techniquement de la rangée 4, en ne tenant pas compte de la première rangée de H et de He, il s'agit de la troisième rangée et elle a un exposant de 1 car il n'y a qu'un seul électron à placer sur l'orbitale d. Nous avons maintenant assigné tous les électrons aux orbitales et suborbitales appropriées, de sorte que la configuration électronique finale complète s'écrit comme suit :

1s ² 2s ² 2p ⁶ 3s ² 3p ⁶ 4s ² 3e ¹

Il s'agit de la version à main longue de sa configuration électronique.

Donc, pour Sc, sa version abrégée de sa configuration électronique serait donc :

[Ar] 4s ² 3e ¹

par Tim

Commencez par déterminer où se situe le titane sur le tableau périodique : ligne 4, groupe 4, ce qui signifie qu'il possède 22 électrons au total. Le titane est un élément à droite du Sc du problème précédent, donc nous utiliserons essentiellement la même méthode sauf qu'à la fin, il restera 2 électrons, donc l'orbitale finale sera désignée comme suit :

3d ²

Si nécessaire, regardez ci-dessus les étapes exactes pour savoir comment procéder à nouveau en détail ; la configuration électronique à main longue pour le titane sera la suivante :

1s ² 2s ² 2p ⁶ 3s ² 3p ⁶ 4s ² 3e ²

Ainsi, pour Ti, sa version abrégée de sa configuration électronique serait donc :

[Ar] 4s ² 3e ²

c. Automobile

Commencez par déterminer où se situe le chrome dans le tableau périodique : ligne 4, groupe 6, ce qui signifie qu'il possède un total de 24 électrons. Mais d'abord, le Cr, ainsi que Mo, Nb, Ru, Rh, Pd, Cu, Sg, Pt et Au, constitue un cas particulier. On pourrait penser qu'étant donné qu'il possède 24 électrons, sa configuration ressemblerait à :

1s ² 2s ² 2p ⁶ 3s ² 3p ⁶ 4s ² 3e ⁴

c'est ainsi que nous l'avons appris tout à l'heure. Cependant, cette configuration électronique est très instable du fait qu'il y a 4 électrons sur son orbite 3D. Les configurations les plus stables sont les orbitales à moitié remplies (d ⁵) et les orbitales complètes (d ¹⁰), de sorte que les éléments dont les électrons se terminent par le d ⁴ ou le d ⁹ sont si instables que nous écrivons leur forme stable à la place, où un électron de l'orbitale s précédente sera déplacé pour remplir l'orbitale d, ce qui a donné une orbitale stable.

Si nécessaire, consultez ci-dessus les étapes exactes pour recommencer la configuration en détail. Cependant, nous devons appliquer la nouvelle règle pour atteindre la stabilité afin que la configuration électronique à longue main du chrome soit la suivante :

1s ² 2s ² 2p ⁶ 3s ² 3p ⁶ 4s ¹ 3d ⁵

Ainsi, pour le Cr, sa version abrégée de sa configuration électronique serait donc :

[Ar] 4s ¹ 3d ⁵

d. Fe

Commencez par déterminer où se situe le fer sur le tableau périodique : ligne 4, groupe 8, ce qui signifie qu'il possède 26 électrons au total. Il s'agit de 5 éléments à droite du Sc du problème précédent, donc nous utiliserons essentiellement la même méthode sauf qu'à la fin, il restera 6 électrons, donc l'orbitale finale sera désignée comme suit :

3d ⁶

Si nécessaire, regardez ci-dessus les étapes exactes pour savoir comment procéder à nouveau en détail ; la configuration des électrons à main longue pour le fer sera la suivante :

1s ² 2s ² 2p ⁶ 3s ² 3p ⁶ 4s ² 3e ⁶

Ainsi, pour Fe, sa version abrégée de sa configuration électronique serait donc :

[Ar] 4s ² 3e ⁶

E. Run

Commencez par déterminer où se situe le ruthénium dans le tableau périodique : ligne 5, groupe 8, ce qui signifie qu'il possède un total de 44 électrons. Mais tout d'abord, comme indiqué précédemment, Ru, ainsi que Cr, Mo, Nb, Rh, Pd, Cu, Sg, Pt et Au, constitue un cas particulier. Comme il possède 44 électrons, on pourrait penser que sa configuration ressemblerait à :

1s ² 2s ² 2p ⁶ 3s ² 3p ⁶ 4s ² 3d ¹⁰ 4p ⁶ 5s ² 4d ⁶

c'est ainsi que nous l'avons appris tout à l'heure. Cependant, cette configuration électronique est très instable du fait que, même s'il existe 4 électrons appariés, il existe également 4 électrons non appariés. Il en résulte une configuration très instable, donc pour rétablir la stabilité, nous devons utiliser une configuration contenant le plus grand nombre d'électrons appariés, qui serait de prendre un électron de l'orbitale s et de le placer sur l'orbitale d pour créer :

5s ¹ 4d ⁷

1s ² 2s ² 2p ⁶ 3s ² 3p ⁶ 4s ² 3d ¹⁰ 4p ⁶ 5s ¹ 4d ⁷

Ainsi, pour le Cr, sa version abrégée de sa configuration électronique serait donc :

[Kr] 5 x ¹ 4 x ⁷

A19.1.1

Sc : [Ar] 4 x ² 3 x ¹
Astuce : [Ar] 4 x ² 3 x ²
Voiture : [Air] 4 vs ¹, 3 x ⁵
Tarif : [Air] 4 x ² x 3 x ⁶
Exécution : [Kr] 5 x ¹ 4 x ⁷ (configuration anormale)

Q19.1.2

Écrivez les configurations électroniques de chacun des éléments suivants et de ses ions :

Ti
Ti ²⁺
Astuce ³⁺
À partir de ^{4 ans}

ARTICLE 19.1.2

Les électrons sont répartis dans des orbitales moléculaires, les$s, p, d, and f$ blocs. Une orbitale sera précédée d'un chiffre et d'une lettre correspondant au bloc. Le bloc s contient deux électrons, le bloc p en contient six, le bloc d en contient dix et le bloc f en contient quatorze. Ainsi, en fonction du nombre d'électrons d'un atome, les orbitales moléculaires sont remplies d'une certaine manière. L'ordre des orbitales est$1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p$. Un exposant sera placé après la lettre de chaque orbitale pour indiquer le nombre d'électrons présents sur cette orbitale. La notation des gaz rares peut également être utilisée en plaçant le gaz noble avant l'élément pour lequel vous écrivez la configuration, puis en écrivant les orbitales remplies après le gaz noble. Les ions métalliques du bloc d verront les deux électrons retirés du bloc s avant que tout électron ne soit retiré du bloc d précédent.

Des solutions :

1. $Ti$

Le titane a un numéro atomique de 22, ce qui signifie qu'il possède 22 électrons. Le gaz noble avant le titane est l'argon. Si l'on regarde la ligne 4 du tableau périodique, le titane a encore 4 électrons à placer sur les orbitales puisque l'argon possède 18 électrons déjà placés. Les électrons restants rempliront l'$4s$orbitale et les deux électrons restants entreront dans l'$3d$orbitale. [Ar] 4s ² 3e ²

2. $Ti^{+2}$

Il s'agit d'un ion avec une charge plus 2, ce qui signifie que 2 électrons ont été retirés. Les électrons seront retirés de l'$4s$orbite et les 2 électrons restants seront placés sur l'$3d$orbitale. Comme le numéro 1, le gaz noble précédent est l'argon. [Art] 3D ²

3. $Ti^{+3}$

Il s'agit d'un ion avec une charge plus 3, ce qui signifie que 3 électrons ont été retirés. Les 2 premiers électrons seront retirés de l'$4s$orbitale, le troisième sera prélevé de l'$3d$orbitale, et le 1 électron restant sera placé sur la 3e orbitale. Comme le numéro 1, le gaz noble précédent est l'argon. [Art] 3e ¹

4. $Ti^{+4}$

Il s'agit d'un ion avec une charge de plus 4, ce qui signifie que 4 électrons ont été retirés. Les 2 premiers électrons seront retirés de l'$4s$orbite et les 2 seconds seront retirés de l'$3d$orbitale. Il en résulte que l'ion a la même configuration électronique que l'argon. [Art]

Réponses :

$[Ar]4s^23d^2$
$[Ar]3d^2$
$[Ar]3d^1$
$[Ar]$

A19.1.2

$[Ar]4s^2 3d^2$
$[Ar]3d^2$
$[Ar]3d^1$
$[Ar]$

Q19.1.3

Écrivez les configurations électroniques de chacun des éléments suivants et de ses ions 3+ :

ARTICLE 19.1.3

Pour écrire la configuration électronique, nous commençons par trouver l'élément sur le tableau périodique. Puisque La, Sm et Lu se situent tous à une période inférieure au xénon, un gaz rare, nous pouvons les abréger${1s^2}{2s^2}{2p^6}{3s^2}{3p^6}{3d^{10}}{4s^2}{4p^6}{4d^{10}}{5s^2}{5p^6}$ en [Xe] lors de l'écriture des configurations orbitales. Nous trouvons ensuite les configurations orbitales restantes en utilisant le principe d'Aufbau. Pour les autres éléments, et pas seulement ceux de la période 6, la notation abrégée utilisant les gaz rares serait le gaz noble de la période au-dessus de l'élément donné.

1. La possède trois électrons supplémentaires. Deux d'entre eux remplissent la coque 6s et l'autre électron est placé sur la coque 5d.

$La:$[Xe]${6{s}^2} {5{d}^1}$

2. Sm a huit électrons supplémentaires. L'orbitale 6s est remplie comme précédemment et l'orbitale 4f reçoit 6 électrons car l'appariement des électrons nécessite moins d'énergie sur la coque 4f que sur la couche 5d.

$Sm:$[Xe]${6{s}^2} {4{f}^6}$

3. Lu a encore dix-sept électrons. Deux électrons remplissent l'orbitale 6s, 14 électrons remplissent l'orbitale 4f et un électron supplémentaire se dirige vers l'orbitale 5d.

$Lu:$[Xe]${6s^2}{4f^{14}}{5d^1}$

Pour trouver la configuration électronique des ions 3+, nous retirons 3 électrons de la configuration neutre, en commençant par l'orbitale 6s.

1. L'ionisation de La ³⁺ élimine les trois électrons supplémentaires. Il revient donc à la configuration stable du xénon.

${La^{3+}:}$[Xe]

2. L'ionisation du Sm ³⁺ élimine deux électrons de la couche 6s et un de la couche la plus externe (4f).

${Sm^{3+}}:$[Xe]${4f^5}$

3. L'ionisation du Lu ³⁺ élimine ses deux couches 6s et une de la coque la plus externe (5d), ne laissant qu'une coque 4f pleine

$Lu^{3+}:$[Xe]$4f^{14}$

A19.1.3

La : [Xe] 6 x ² 5 d ¹, La ³⁺ : [Xe] ; Sm : [Xe] 6 x ² 4 f ⁶, Sm ³⁺ : [Xe] 4 f ⁵ ; Lu : [Xe] 6 x ² 4 f ¹⁴ 5 d ¹, Luc ³⁺ : [Xe] 4 de ¹⁴

Q19.1.4

Pourquoi les éléments lanthanides ne se trouvent-ils pas dans la nature sous leurs formes élémentaires ?

A19.1.4

Les lanthanides se trouvent rarement sous leurs formes élémentaires parce qu'ils transmettent facilement leurs électrons à d'autres éléments plus électronégatifs, formant des composés au lieu de rester sous une forme élémentaire pure. Ils ont des propriétés chimiques très similaires les uns aux autres, se trouvent souvent dans les profondeurs de la terre et sont difficiles à extraire. Ce sont les éléments de transition internes et ont des orbitales d partiellement remplies qui peuvent donner des électrons. De ce fait, ils sont très réactifs et électropositifs.

Q19.1.5

Lequel des éléments suivants est le plus susceptible d'être utilisé pour préparer La par réduction de La ₂ O ₃ : Al, C ou Fe ? Pourquoi ?

ARTICLE 19.1.5

Une série d'activités est une liste d'éléments classés par ordre décroissant de leur réactivité. Les éléments du haut de la liste sont de bons agents réducteurs car ils abandonnent facilement un électron, et les éléments du bas de la série sont de bons agents oxydants parce qu'ils sont hautement électronégatifs et voudraient vraiment accepter un électron.

Étape 1 : Comparez l'aluminium, le carbone et le fer sur une série d'activités. De nombreuses séries d'activités incluent le carbone et l'hydrogène comme références. Une série d'activités peut être consultée ici

La série d'activités se déroule dans l'ordre (de haut en bas) : aluminium, carbone et fer.

Étape 2 : Identifiez quel élément est le meilleur agent réducteur.

Les éléments en haut de la liste sont les meilleurs agents réducteurs, car ce sont eux qui donnent le mieux des électrons.

L'aluminium est le meilleur agent réducteur parmi les options disponibles.

L'aluminium sera donc le meilleur agent réducteur pour préparer La par réduction de La ₂ O ₃, car il est le plus réactif de la série parmi les trois éléments.

A19.1.5

L'Al est utilisé parce que c'est l'agent réducteur le plus puissant et la seule option répertoriée qui peut fournir une force motrice suffisante pour convertir La (III) en La.

Q19.1.6

Lequel des agents suivants est l'agent oxydant le plus puissant :$\ce{VO4^{3-}}$,$\ce{CrO4^2-}$, ou$\ce{MnO4-}$ ?

ARTICLE 19.1.6

Les agents oxydants oxydent d'autres substances. En d'autres termes, ils gagnent des électrons ou se réduisent. Ces agents doivent être dans leur état d'oxydation le plus élevé. Afin de déterminer la force des composés ci-dessus en tant qu'agents oxydants, déterminez le nombre d'oxydation de chaque élément constitutif.

$\\\mathrm{VO_4^{3-}}$

Nous savons qu'il$\mathrm{O}$ a un état d'oxydation -2 et que la charge globale de l'ion est de -3. Nous avons juste besoin de déterminer l'indice d'oxydation du vanadate dans ce composé.

$\\\mathrm{V} + \mathrm{-2(4)} = \mathrm{-3}$

$\\\mathrm{V} = \mathrm{+5}$

Le vanadate a un indice d'oxydation de +5, qui est son état d'oxydation le plus élevé possible.

$\\\mathrm{CrO_4^{2-}}$

Comme dans le calcul précédent,$\mathrm{O}$ possède un état d'oxydation -2. La charge globale est de -2. Calculez donc pour le chrome.

$\\\mathrm{Cr} + \mathrm{-2(4)} = \mathrm{-2}$

$\\\mathrm{Cr} = \mathrm{+6}$

Le chrome est dans son état d'oxydation le plus élevé possible (+6) dans ce composé.

$\\\mathrm{MnO_4^-}$

$\mathrm{O}$a un état d'oxydation -2 et la charge globale est de -1.

$\\\mathrm{Mn} + \mathrm{-2(4)} = \mathrm{-1}$

$\\\mathrm{Mn} = \mathrm{+7}$

Le manganèse est également dans son état d'oxydation le plus élevé, +7.

Un agent oxydant doit être capable de gagner des électrons qui, à leur tour, réduisent son état d'oxydation. Ici, le manganèse possède l'état d'oxydation le plus élevé, ce qui lui permet de subir une plus grande diminution de son état d'oxydation si nécessaire, ce qui signifie qu'il peut gagner le plus d'électrons. Donc, parmi les trois composés,$\mathrm{MnO_4^-}$ se trouve l'agent oxydant le plus puissant. Cette méthode suppose que les métaux ont des électronégativités similaires.

Vous pouvez également consulter un tableau redox.

A19.1.6

$MnO_4^-$

Q19.1.7

Lequel des éléments suivants est le plus susceptible de former un oxyde de formule MO ₃ : Zr, Nb ou Mo ?

ARTICLE 19.1.7

Mo parce que Zr a un état d'oxydation de +4 et que le Nb a un état d'oxydation de +5 et que ceux-ci n'équilibreraient pas la charge de 3 oxygènes à l'état -2, ce qui crée une charge de -6. Mo possède cependant plusieurs états d'oxydation, le plus courant étant +6 qui équilibre la charge -6 créée par 3 ions oxygène. C'est pourquoi il est plus susceptible de former un oxyde de formule MO ₃ ou$\ce{MoO3}$.

A19.1.7

Q19.1.8

Les réactions suivantes se produisent toutes dans un haut fourneau. Lesquelles de ces réactions sont des réactions redox ?

$\ce{3Fe2O3}(s)+\ce{CO}(g)⟶\ce{2Fe3O4}(s)+\ce{CO2}(g)$
$\ce{Fe3O4}(s)+\ce{CO}(g)⟶\ce{3FeO}(s)+\ce{CO2}(g)$
$\ce{FeO}(s)+\ce{CO}(g)⟶\ce{Fe}(l)+\ce{CO2}(g)$
$\ce{C}(s)+\ce{O2}(g)⟶\ce{CO2}(g)$
$\ce{C}(s)+\ce{CO2}(g)⟶\ce{2CO}(g)$
$\ce{CaCO3}(s)⟶\ce{CaO}(s)+\ce{CO2}(g)$
$\ce{CaO}(s)+\ce{SiO2}(s)⟶\ce{CaSiO3}(l)$

S19.1.8

Pour identifier la réaction redox, nous devons déterminer s'il faut voir si l'équation est une réaction d'oxydoréduction, c'est-à-dire que les espèces changent d'état d'oxydation au cours de la réaction, ce qui implique le transfert d'électrons entre deux espèces. Si une espèce perd des électrons, c'est qu'elle est oxydée. Si une espèce gagne des électrons, alors cette espèce est réduite. Une façon de s'en souvenir est d'utiliser les acronymes OIL RIG. L'oxydation I est la perte de L et la réduction de R est le gain de G, en référence aux électrons. Ces deux éléments doivent se produire pour qu'une équation soit une réaction d'oxydoréduction. Voyons si ces équations sont des réactions redox ou non :

a. Du côté des réactifs$\ce{Fe2O3}$, le Fe a un indice d'oxydation de +3. Dans le produit$\ce{Fe3O4}$, le Fe a un indice d'oxydation de +2,67. Puisque le Fe est passé de +3 à +2,67, on peut dire que le Fe a gagné des électrons et a donc diminué. Dans le réactif, le CO, le carbone a un indice d'oxydation de +2, et dans$\ce{CO2}$ (le produit), le carbone a un indice d'oxydation de +4. Par conséquent, le carbone a perdu des électrons et s'est oxydé. Comme il y a oxydation et réduction des espèces, nous pouvons conclure qu'il s'agit d'une réaction redox.

b. Dans le réactif$\ce{Fe3O4}$, le Fe a un indice d'oxydation de +2,67. Dans le produit, le FeO et le Fe ont un indice d'oxydation de +2. Comme l'oxydation du Fe est passée de +2,67 à +2, des électrons ont été ajoutés, donc le Fe a été réduit. Dans le réactif, le CO, le carbone a un indice d'oxydation de +2, et dans$\ce{CO2}$ (le produit), le carbone a un indice d'oxydation de +4. Par conséquent, le carbone a perdu des électrons et s'est oxydé. Comme il y a oxydation et réduction des espèces, nous pouvons conclure qu'il s'agit d'une réaction redox.

c. Du côté des réactifs, dans le FeO, le Fe a un indice d'oxydation de +2 et du côté des produits, le Fe a un indice d'oxydation de 0. Comme le nombre d'oxydation du Fe est passé de +2 à 0, des électrons ont été gagnés et donc du Fe a été réduit. Dans le réactif, le CO, le carbone a un indice d'oxydation de +2, et dans$\ce{CO2}$ (le produit), le carbone a un indice d'oxydation de +4. Par conséquent, le carbone a perdu des électrons et s'est oxydé. Comme il y a oxydation et réduction des espèces, nous pouvons conclure qu'il s'agit d'une réaction redox.

d. Dans les réactifs, C a un indice d'oxydation de 0, et dans le côté des produits$\ce{CO2}$, C a un indice d'oxydation de +4. Puisque le nombre d'oxydation de C est passé de 0 à +4, on peut dire que C a été oxydé. Dans les réactifs, l'$\ce{O2}$oxygène a un indice d'oxydation de 0, et dans les produits CO2, l'oxygène a un indice d'oxydation de -2. Comme l'indice d'oxydation de l'oxygène est passé de 0 à -2, l'oxygène a été réduit. Comme il y a oxydation et réduction des espèces, nous pouvons conclure qu'il s'agit d'une réaction redox.

e. Dans les réactifs$\ce{CO2 }$ a un indice d'oxydation de +4, et dans le côté des produits dans le CO, C a un indice d'oxydation de +2. Depuis que le carbone est passé de +4 à +2, le carbone a été réduit. Dans les réactifs, l'$\ce{CO2 }$oxygène a un indice d'oxydation de -4 et dans les produits, le carbone CO a un indice d'oxydation de -2. Comme l'oxygène est passé de -4 à -2, il s'est oxydé. Comme il y a oxydation et réduction des espèces, nous pouvons conclure qu'il s'agit d'une réaction redox.

f. Dans les réactifs, le$\ce{CaCO3}$ Ca a un indice d'oxydation de +2, et dans les produits, le CaO Ca a un indice d'oxydation de +2. Puisque le nombre d'oxydation ne change pas, nous pouvons en conclure que cette équation n'est pas une réaction d'oxydoréduction.

g. Dans les produits, CaO Ca a un indice d'oxydation de +2, et dans les produits,$\ce{CaSiO3}$ Ca a un indice d'oxydation de +2. Puisque le nombre d'oxydation ne change pas, nous pouvons en conclure que cette équation n'est pas une réaction d'oxydoréduction.

A19.1.8

a, b, c, d, e

Q19.1.9

Pourquoi la formation de scories est-elle utile lors de la fusion du fer ?

S19.1.9

Le laitier est une substance formée comme sous-produit de la fusion de minerai de fer ou de granulés de fer dans un haut fourneau. Le laitier est également le sous-produit qui se forme lorsqu'un métal souhaité a été séparé de son minerai brut. Il est important de noter que les scories des aciéries sont créées de manière à réduire la perte du minerai de fer souhaité. Les$\ce{CaSiO3}$ scories sont moins denses que le fer fondu, elles peuvent donc être facilement séparées. De plus, la couche de scorie flottante crée une barrière qui empêche l'exposition au fer fondu$\ce{O2}$, ce qui oxyderait le$\ce{Fe}$ dos$\ce{Fe2O3}$. Comme le Fe a un faible potentiel de réduction de -0,440, cela signifie qu'il a un potentiel d'oxydation élevé, de sorte qu'il s'oxyderait facilement en présence d'O2. La création d'une barrière entre le fer et l'oxygène permet d'obtenir le maximum de produit de fer à la fin de la fusion.

A19.1.9

Le laitier CaSIO ₃ est moins dense que le fer fondu, il peut donc être facilement séparé. De plus, la couche de laitier flottante crée une barrière qui empêche le fer fondu d'être exposé à l'O ₂, ce qui oxyderait le Fe en Fe ₂ O ₃.

Q19.1.10

Vous attendez-vous à ce qu'une solution aqueuse d'oxyde de manganèse (VII) ait un pH supérieur ou inférieur à 7,0 ? Justifiez votre réponse.

S19.1.10

L'oxyde de manganèse (VII) peut être écrit Mn ₂ O _7.

En relation avec la théorie acide-base de Lewis, un acide de Lewis accepte des électrons à paire unique et est également connu sous le nom d'accepteur de paires d'électrons. Sur la base de cette théorie, l'acidité peut être mesurée par la capacité de l'élément à accepter des paires d'électrons. En faisant le calcul, nous découvrons que le manganèse a un état d'oxydation de +7 (l'oxygène a un état d'oxydation de -2, et 2x-7 = -14 ou cela peut être montré au fur$-7(2)+2(x)=0$ et à$x=7$ mesure que le composé entier a une charge nulle, pour équilibrer la charge de l'ion, Mn doit être de +7). Par conséquent, le Mn a une grande capacité à accepter des électrons en raison de sa charge positive élevée. Pour la plupart des métaux, à mesure que le nombre d'oxydation augmente, leur acidité augmente également, en raison de leur capacité accrue à accepter les électrons.

A19.1.10

En relation avec la théorie acide-base de Lewis, l'acide de Lewis accepte des électrons à paire unique ; il est donc également connu sous le nom d'accepteur de paires d'électrons. Il peut s'agir de n'importe quelle espèce chimique. Les acides sont des substances qui doivent être inférieures à 7. Par conséquent, les oxydes de manganèse vont probablement devenir plus acides dans les solutions (aq) si le nombre d'oxydation augmente.

Q19.1.11

Le fer (II) peut être oxydé en fer (III) par l'ion dichromate, qui est réduit en chrome (III) dans une solution acide. Un échantillon de 2 500 g de minerai de fer est dissous et le fer converti en fer (II). Exactement 19,17 ml de 0,0100 M de Na ₂ Cr ₂ O ₇ à 0,0100 M sont nécessaires pour le titrage. Quel pourcentage de l'échantillon de minerai était constitué de fer ?

S19.1.11

Pour répondre à cette question, nous devons d'abord identifier l'équation ionique nette à partir des demi-réactions données. On peut écrire les demi-réactions d'oxydation et de réduction :

\[ \text{ oxidation:} \text{ Fe}^\text{ 2+} \rightarrow \text{ Fe}^\text{ 3+} \]

\[ \text{ reduction: }\ce{Cr2O7^2-} \rightarrow \text{ Cr}^\text{ 3+} \]

Nous pouvons rapidement équilibrer la demi-réaction d'oxydation en ajoutant le nombre approprié d'électrons pour obtenir

\[ \text{ Fe}^\text{ 2+} \rightarrow \text{ Fe}^\text{ 3+}+\text{ e}^- \]

La première étape pour équilibrer la demi-réaction de réduction consiste à équilibrer les éléments de l'équation autres que O et H. Ce faisant, nous obtenons

\[\ce{Cr2O7^2-} \rightarrow 2 \text{ Cr}^\text{ 3+} \]

La deuxième étape serait d'ajouter suffisamment de molécules d'eau pour équilibrer l'oxygène.

\[ \ce{Cr2O7^2-} \rightarrow 2 \text{ Cr}^\text{ 3+}+ \ce{7H2O} \]

Ensuite, nous ajoutons la bonne quantité de H ⁺ pour équilibrer les atomes d'hydrogène.

\[ \ce{Cr2O7^2-}+14 \text{ H}^+ \rightarrow 2 \text{ Cr}^\text{ 3+}+ \ce{7H2O} \]

Enfin, nous ajoutons suffisamment d'électrons pour équilibrer la charge.

\[ \ce{Cr2O7^2-}+14 \text{ H}^++6 \text{ e}^- \rightarrow 2 \text{ Cr}^\text{ 3+}+ \ce{7H2O} \]

Les électrons impliqués dans les deux demi-réactions doivent être égaux pour que nous puissions combiner les deux et obtenir l'équation ionique nette. Cela peut être fait en multipliant chaque équation par le coefficient approprié. En multipliant par 6 la demi-réaction d'oxydation, nous obtenons

\[ 6 \text{ Fe}^\text{ 2+} \rightarrow 6 \text{ Fe}^\text{ 3+}+6 \text{ e}^- \]

Nous pouvons maintenant combiner les deux demi-réactions pour obtenir

\[ 6 \text{ Fe}^\text{ 2+}+\ce{Cr2O7^2-}+14 \text{ H}^++6 \text{ e}^- \rightarrow 6 \text{ Fe}^\text{ 3+}+6 \text{ e}^-+2 \text{ Cr}^\text{ 3+}+ \ce{7H2O}\]

Les électrons s'annulent, donc vous obtenez :

\[ 6 \text{ Fe}^\text{ 2+}+\ce{Cr2O7^2-}+14 \text{ H}^+ \rightarrow 6 \text{ Fe}^\text{ 3+}+2 \text{ Cr}^\text{ 3+}+ \ce{7H2O}\]

Nous pouvons en déduire que le rapport molaire entre le Cr ₂ O ₇ ^2- et le Fe ²⁺ est de 1:6. Étant donné que 19,17 ml (ou 0,01917 L) de 0,01 M de Na ₂ Cr ₂ O ₇ étaient nécessaires pour le titrage, nous savons que

\[ 0.01917\text{ L} \times 0.01 \text{ M} = 1.917 \times 10^{-4} \text{ mol} \]

g de Na ₂ Cr ₂ O ₇ ont réagi. De plus, étant donné qu'un nombre quelconque de moles de Na ₂ _{Cr 2} O ₇ produit le même nombre de moles de Cr ₂ O ₇ ^2- en solution

\[ 1.917 \times 10^{-4} \text{ mol} \text{ of } \ce{Na2Cr2O7} =1.917 \times 10^{-4} \text{ mol} \text{ of } \ce{Cr2O7^2-}\]

Nous pouvons utiliser le rapport molaire entre le Cr ₂ O ₇ ^2- et le Fe ²⁺ pour déterminer le nombre de moles de fer (ii) présentes dans la solution. Le nombre de moles de fer (ii) est le même que le nombre de moles de fer pur dans l'échantillon puisque tout le fer a été converti en fer (ii).

\[ 1.917 \times 10^{-4} \text{ mol} \text{ of } \ce{Cr2O7^2-}\times \frac{6\text{ mol}\text{ of } \text{ Fe}^\text{ 2+}}{1\text{ mol}\text{ of }\ce{Cr2O7^2-}} = 0.0011502\text{ mol}\text{ of } \text{ Fe}^\text{ 2+} \]

\[ 0.0011502\text{ mol}\text{ of } \text{ Fe}^\text{ 2+} = 0.0011502\text{ mol}\text{ of } \text{ Fe} \]

Nous pouvons maintenant déterminer le nombre de grammes de fer présents dans l'échantillon de 2,5 g de minerai de fer.

\[ 0.0011502\text{ mol}\text{ of } \text{ Fe}\times\frac{55.847\text { g}}{1\text{ mol}} = 0.0642352194\text{ g}\text{ of }\text{ Fe} \]

Enfin, nous pouvons répondre à la question et déterminer quel pourcentage de l'échantillon de minerai était constitué de fer.

\[ \frac{0.0642352194\text{ g}}{2.5\text{ g}} \times 100 \approx 2.57\text{%} \]

Donc, 2,57 % de l'échantillon de minerai était du fer.

A19.1.11

2,57 %

Q19.1.12

Combien de pieds cubes d'air à une pression de 760 torr et à 0 °C sont nécessaires par tonne de Fe ₂ O ₃ pour convertir ce Fe ₂ O ₃ en fer dans un haut fourneau ? Pour cet exercice, supposons que l'air contient 19 % d'oxygène par volume.

S19.1.12

Cette question utilise une série de conversions d'unités et l'$PV=nRT$équation.

La première étape consiste à écrire l'équation chimique équilibrée pour la conversion du Fe ₂ O ₃ en fer pur.

\[2\;Fe_2O_3(s)\rightarrow 4\;Fe(s)+3\;O_2(g)\]

Ensuite, nous devons analyser la question initiale afin de déterminer la valeur à résoudre. Comme la question demande une valeur en pieds cubes, nous savons que nous devons résoudre le problème du volume. Nous pouvons manipuler$PV=nRT$ pour résoudre le problème du volume.

\[V={nRT}/P\]

Déterminez maintenant les variables connues et convertissez-les en unités faciles à gérer.

\[n = 2000\:lbs\; Fe_2O_3\frac{453.592\: grams\: Fe_2O_3}{1\: lb \:Fe_2O_3}\frac{1\: mole \:Fe_2O_3}{159.69\: grams \:Fe_2O_3}\frac{3 \;moles\: O_2}{2\; moles \:Fe_2O_3}\]

\[n=8521\: moles\: of \:O_2\]

Convertir en ATM pour faciliter les calculs

\[R=\frac{.0821\:L\:atm}{mol\:K}\]

\[T=0^{\circ}C=273\:K\]

\[P=760 \:torr= 1 \:atm\]

Maintenant, insérez les chiffres dans la loi sur les gaz manipulée pour obtenir une réponse pour V.

\[V=190991.8\: liters \:of\: O_2\]

De là, nous convertissons les litres en pieds cubes.

utiliser la conversion

\[1\;L=.0353 ft^3\]

nous avons donc 6744,811 pieds ³ de O ₂

Nous revenons ensuite à la question initiale et rappelons que cette valeur ne représente que 19 % du volume de l'air total. Utilisez donc une équation simple pour déterminer le volume total d'air en pieds cubes.

\[6744.811ft^3=.19x\]

x=35499 pieds ³ d'air

A19.1.12

35499 pieds ³ d'air

Q19.1.13

Déterminez les potentiels de la cellule électrochimique suivante :

Cd | Cd ²⁺ (M = 0,10) ▷ Ni ²⁺ (M = 0,50) | Ni

S19.1.13

Étape 1 Écrivez vos deux demi-réactions et identifiez laquelle est l'oxydation et laquelle est la réduction en utilisant l'acronyme OIL RIG pour vous rappeler que l'oxydation est une perte d'électrons et que la réduction est un gain d'électrons.

Cd (s) Cd ²⁺ (aq) +2e ^- (oxydation)

Ni ²⁺ (aq) +2e ^- Ni (s) (réduction)

Étape 2 Écrivez l'équation équilibrée complète

Cd (s) + Ni ²⁺ (aq) Cd ²⁺ (aq) +Ni (s)

Étape 3 : Trouvez E ^sur _{une cellule}

_Cellule E ^o = _cathode E - _anode E

oxydation : Cd (s) Cd ²⁺ (aq) +2e ^- E ^o =-0,40V

réduction : Ni ²⁺ (aq) +2e ^- Ni (s) E ^o =-0,26 V

* Les valeurs E proviennent du tableau des potentiels de réduction standard présenté ci-dessus. N'oubliez pas non plus que l'anode est l'endroit où se produit l'oxydation et la cathode où se produit la réduction.

E ^ou cellule=-0,26- (-0,40)

E ^ou _cellule = 0,14 V

Étape 4 Trouvez Q

Q= [produits]/[réactifs] (regardez l'équation équilibrée complète) (rappelez-vous que [x] signifie la concentration de x généralement donnée en molarité et que nous ignorons les solides ou les liquides)

Q= [Cd ²⁺]/[Ni ²⁺]

Q=0,10/0,50

Q=0,2

Étape 5 Calculez E en utilisant E = E ^o _cell - (0,0592/n) LogQ (n est le nombre de moles d'électrons transférées et, dans notre cas, la réaction équilibrée transfère 2 électrons)

E = 0,14- (0,0592/2) log (0,2)

E = 0,14- (-0,207)

E=0,16 V

A19.1.13

0,16 V

Q19.1.14

Un échantillon de 2,5624 g de chlorure de métal alcalin solide pur est dissous dans de l'eau et traité avec un excès de nitrate d'argent. Le précipité obtenu, filtré et séché, pèse 3,03707 g. Quel était le pourcentage en masse d'ions chlorure dans le composé d'origine ? Quelle est l'identité du sel ?

S19.1.14

En supposant que le chlorure métallique est XCl

L'équation d'équilibre pour la réaction serait la suivante :

\[XCl(aq)+AgNO_{3}(aq)\rightarrow XNO_{3}(aq) +AgCl(s)\]

La masse d'AgCl = 3,03707 g

Pour trouver les moles d'AgCl présentes :

Ensuite, nous pouvons déterminer les moles d'AgCl présentes dans la réaction puisque 1) la masse du précipité nous est donnée et 2) cette valeur peut nous aider à déterminer les moles du composé de chlorure de métal alcalin présent. Étant donné que la masse d'AgCl est de 3,03707 g dans le problème et que la masse moléculaire d'AgCl par mole est de 143,32 g, nous pouvons déterminer le nombre de moles d'AgCl présentes dans la réaction :

\[moles of Agcl=\tfrac{3.03707g}{143.32g/mol}=0.0211 mol\]

Comme le rapport molaire des composés est de 1:1, le nombre de moles de XCl utilisées est donc de 0,0211 mol

Nous pouvons calculer le poids de Cl ^- avec l'équation suivante :

\[0.0211 mol \times 35.5g/mol = 0.7490g\]

la quantité de métal présente dans le composé d'origine est le poids du composé soustrait en poids de l'ion Cl :

\[(2.5624- 0.7490)g= 1.8134g\]

Et le pourcentage peut être calculé par

\[\frac{0.7490}{2.5624}\times 100= 29.23 \%\]

le rapport molaire de XCl est de 1:1 donc

Masse atomique du métal =$=\frac{1.8134\;g\; metal}{0.0211\; mol\; RbCl}=85.943g/mol$

La masse atomique est donc de 85,943 g/mol, qui est de Rb, d'où l'identité du sel est RbCl.

Q19.1.15

Le potentiel de réduction standard de la réaction$\ce{[Co(H2O)6]^3+}(aq)+\ce{e-}⟶\ce{[Co(H2O)6]^2+}(aq)$ est d'environ 1,8 V. Le potentiel de réduction de la réaction$\ce{[Co(NH3)6]^3+}(aq)+\ce{e-}⟶\ce{[Co(NH3)6]^2+}(aq)$ est de +0,1 V. Calculez les potentiels cellulaires pour montrer si les ions complexes, [Co (H ₂ O) ₆] ²⁺ et/ou [Co (NH ₃) ₆] ²⁺, peut être oxydé en complexe de cobalt (III) correspondant par l'oxygène.

S19.1.15

Pour calculer le potentiel cellulaire, nous devons connaître les potentiels de chaque demi-réaction. Ensuite, nous devons déterminer lequel est oxydé et lequel est réduit. Celle qui est oxydée est l'anode et celle qui est réduite est la cathode. Pour déterminer le potentiel cellulaire, vous devez utiliser cette formule et les valeurs du potentiel de réduction figurant dans un tableau des potentiels de réduction. Si la cellule E° est positive,$\Delta$ G est négative et la réaction est spontanée.

Cellule E° = E°cathode - E°anode

Comme il indique qu'il$[Co(H_{2}O)_{6}]^{3+}$ sera oxydé, cela signifie qu'il s'agit de l'anode.

$O_{2}(g) + 4 H^{+}(aq) + 4 e^{-} \rightarrow 2 H_{2}O$+1,229 V

$O_{2}$est en train d'être réduite, donc c'est la cathode.

1,229 V - 1,8 V = -0,571 V, ou -0,6 V en utilisant des chiffres significatifs. Cela ne peut pas se produire spontanément car la cellule E° est négative.

Car$[Co(NH_{3})_{6}]^{3+}$ elle est à nouveau oxydée, c'est-à-dire que c'est l'anode.

1,229 à 0,1 = 1,129 V ou 1,1 V en utilisant des chiffres significatifs. Cette réaction est spontanée car la cellule E° est positive.

A19.1.15

a) E° = −0,6 V, E° est négatif, donc cette réduction n'est pas spontanée.

b) E° = +1,1 V, E° est positif donc cette réduction est spontanée.

Q19.1.16

Prédisez les produits de chacune des réactions suivantes. (Remarque : En plus d'utiliser les informations de ce chapitre, utilisez également les connaissances que vous avez accumulées à ce stade de votre étude, y compris les informations sur la prédiction des produits de réaction.)

$\ce{MnCO3}(s)+\ce{HI}(aq)⟶$
$\ce{CoO}(s)+\ce{O2}(g)⟶$
$\ce{La}(s)+\ce{O2}(g)⟶$
$\ce{V}(s)+\ce{VCl4}(s)⟶$
$\ce{Co}(s)+xs\ce{F2}(g)⟶$
$\ce{CrO3}(s)+\ce{CsOH}(aq)⟶$

S19.1.16

Une myriade de réactions peuvent se produire, notamment : remplacement unique, double remplacement, combustion, acide/neutralisation, décomposition ou synthèse. La première étape pour déterminer les produits d'une réaction consiste à identifier le type de réaction. À partir de ce moment, les prochaines étapes à suivre pour prévoir les produits varieront en fonction du type de réaction.

Cette réaction est une réaction à double déplacement, dans laquelle les cations et les anions des réactifs changent de place pour former de nouveaux composés. Écrire l'équation en termes d'ions aqueux vous aidera à visualiser exactement ce qui se déplace :
\[2H^{+}(aq)+2I^{-}(aq)\rightarrow 2H^{+}(aq)+CO_{3}^{2-}(aq)+Mn^{2+}(aq)+2I^{-}(aq)\]
dans ce cas, les cations hydrogène se recombineront avec des anions carbonate tandis que les cations manganèse se recombineront avec des anions iodure, ce qui nous donnera le équation suivante :
\[\ce{MnCO3}(s)+\ce{2HI}(aq)⟶\ce{MnI2}(aq)+\ce{H2CO3}(aq)\]
Ce n'est toujours pas la réponse finale, car l'acide carbonique est instable et se décompose en dioxyde de carbone et en eau dans des conditions standard. En tenant compte de cela, notre équation finale est la suivante :
\[\ce{MnCO3}(s)+\ce{2HI}(aq)⟶\ce{MnI2}(aq)+\ce{CO2}(g)+\ce{H2O}(l)\]
Cette réaction est une réaction de synthèse dans laquelle deux réactifs ou plus se combinent pour former un composé plus complexe. Dans ce cas, nous faisons également réagir un oxyde métallique avec de l'oxygène, ce qui produirait un autre oxyde métallique comme produit. Le produit résultant serait l'oxyde de valence mixte Co ₃ O ₄ dans lequel un atome de cobalt possède un état d'oxydation +2 tandis que les deux autres ont un état d'oxydation +3. Il ne reste plus qu'à équilibrer l'équation :
\[\ce{6CoO}(s)+\ce{O2}(g)⟶\ce{2Co3O4}(s)\]
Comme l'équation 2, cette réaction est également une réaction de synthèse impliquant un métal et de l'oxygène qui devrait entraîner la formation d'un oxyde métallique. Il s'agit maintenant d'équilibrer les états d'oxydation pour obtenir un composé neutre. L'oxygène conservera toujours un état d'oxydation -2 dans les composés tandis que le lanthane présentera toujours un état d'oxydation +3. Ainsi, une combinaison de 2 atomes de lanthane avec un état d'oxydation +3 et de 3 atomes d'oxygène avec un état d'oxydation -2 nous donnera une molécule avec une charge globale de 0 (3 (-2) +2 (+3) =0). Nous connaissons maintenant notre produit, La ₂ O ₃, et il ne nous reste plus qu'à équilibrer l'équation globale, en nous donnant :
\[\ce{4La}(s)+\ce{3O2}(g)⟶\ce{2La2O3}(s)\]
Cette réaction est légèrement plus difficile à définir car elle englobe à la fois les propriétés des réactions de synthèse et de décomposition, dans lesquelles le vanadium réagit avec le tétrachlorure de vanadium pour produire du trichlorure de vanadium. Cette réaction est toutefois principalement une réaction de synthèse puisque nous combinons deux réactifs pour produire un composé complexe. En utilisant le trichlorure de vanadium comme produit, nous pouvons équilibrer l'équation :
\[\ce{V}(s)+\ce{3VCl4}(s)⟶\ce{4VCl3}(s)\]
Il s'agit d'une autre réaction de synthèse associant le cobalt et le fluor. Cette équation inclut la notation « xs » devant le fluor, abréviation de « excès », ce qui signifie qu'il y a plus de fluor que ce qui est réellement nécessaire dans les réactifs, garantissant ainsi la fin de la réaction. Pour trouver les produits, il suffit de combiner le cobalt et le fluor en une seule molécule, ce qui nous laisse déjà avec une équation équilibrée :
\[\ce{Co}(s)+xs\ce{F2}(g)⟶\ce{CoF2}(s)\]
Ce n'est peut-être pas évident ici, mais la réaction qui nous a été donnée ici est en fait une réaction acide-base/neutralisation, avec du trioxyde de chrome agissant comme acide et de l'hydroxyde de césium comme base. Le trioxyde de chrome est appelé oxyde acide, ce qui signifie qu'il réagira avec l'eau pour former un acide. Notez que cette réaction peut toujours se produire même si les réactifs ne sont pas dans les mêmes phases. La règle de base pour les réactions acide-base/neutralisation est qu'elles forment un sel (sel étant le terme général désignant tout composé ionique formé à partir de réactions acide-base) et de l'eau. Comme nous savons que l'eau est l'un de nos produits, notre autre produit doit être un sel composé de césium, de chrome et d'oxygène. Ainsi, notre autre produit devrait être le chromate de césium, et vous pouvez maintenant équilibrer l'équation en conséquence :
\[\ce{CrO3}(s)+\ce{2CsOH}(aq)⟶\ce{Cs2CrO4}(aq)+\ce{H2O}\]

A19.1.16

$\ce{MnCO3}(s)+\ce{2HI}(aq)⟶\ce{MnI2}(aq)+\ce{CO2}(g)+\ce{H2O}(l)$
$\ce{6CoO}(s)+\ce{O2}(g)⟶\ce{2Co3O4}(s)$
$\ce{4La}(s)+\ce{3O2}(g)⟶\ce{2La2O3}(s)$
$\ce{V}(s)+\ce{3VCl4}(s)⟶\ce{4VCl3}(s)$
$\ce{Co}(s)+xs\ce{F2}(g)⟶\ce{CoF2}(s)$
$\ce{CrO3}(s)+\ce{2CsOH}(aq)⟶\ce{Cs2CrO4}(aq)+\ce{H2O}$

Q19.1.17

$\ce{Fe}(s)+\ce{H2SO4}(aq)⟶$
$\ce{FeCl3}(aq)+\ce{NaOH}(aq)⟶$
$\ce{Mn(OH)2}(s)+\ce{HBr}(aq)⟶$
$\ce{Cr}(s)+\ce{O2}(g)⟶$
$\ce{Mn2O3}(s)+\ce{HCl}(aq)⟶$
$\ce{Ti}(s)+xs\ce{F2}(g)⟶$

S19.1.17

Prédisez les produits de chacune des réactions suivantes.

Frais (s) +H ₂ SO ₄ (aq) ⟶ ?

Chaque fois qu'un métal réagit avec un acide, les produits sont du sel et de l'hydrogène. Comme le Fe se situe plus bas dans la série d'activités, nous savons que lorsqu'il réagit avec un acide, il entraîne la formation d'hydrogène gazeux. Pour simplifier l'équation, il suffit de :

\[Metal + Acid ⟶ Salt + Hydrogen\]

Le sel produit dépend du métal et, dans ce cas, le métal est le fer (Fe), donc l'équation résultante serait la suivante :

\[\ce{Fe}(s)+\ce{H2SO4}(aq)⟶ \ce{FeSO4}(aq) + \ce{H2}(g)\]

Cette équation fonctionne lorsque le H2 est retiré de H _{2 SO ₂}, ce qui donne un ion SO ₄ ^2- où le Fe prendra un état d'oxydation de Fe ⁺² pour former du FeSO ₄ qui sera le sel dans cet exemple.

Mais comme le FeSO ₄ et le H2SO ₄ sont aqueux, les réactifs et les produits peuvent également être écrits sous forme d'ions, où l'équation globale peut être :

\[\ce{Fe}(s)+\ce{2H3O+}(aq)+\ce{SO2^{−4}}(aq)⟶\ce{Fe2+}(aq)+\ce{SO2^{−4}}(aq)+\ce{H2}(g)+\ce{2H2O}(l)\]

FeCl ₃ (aq) +NaOH (aq) ⟶ ?

Dans ce cas, l'ajout d'un hydroxyde métallique (NaOH) à une solution contenant un ion de métal de transition (Fe) formera un hydroxyde de métal de transition (XOH). Comme le fer est lié à trois atomes de chlore du côté des réactifs, il a un état d'oxydation de +3, où trois ions hydroxyde (OH ^-) sont nécessaires pour équilibrer les charges lorsqu'ils sont liés dans les produits. ^{Les ions restants sont Na ⁺ et Cl, où ils se lient ensemble dans un rapport de 1:1 où il y a 3 molécules de NaCl une fois la réaction équilibrée.}

La réaction globale sera la suivante :

\[\ce{FeCl3}(aq)+\ce{NaOH}(aq)⟶ \ce{Fe(OH)3}(s) + \ce{3NaCl}(aq)\]

REMARQUE : Le Fe (OH) ₃ (s) est un solide car, en règle générale, tous les hydroxydes de métaux de transition sont insolubles et un précipité se forme.

Puisque le NaOH (aq) et le NaCl (aq) sont aqueux, nous pouvons les écrire sous leurs formes ioniques :

\[\ce{FeCl3}(aq)+\ce{3Na+}(aq)+\ce{3OH^{−}}(aq)+\ce{Fe(OH)3}(s)+\ce{3Na+}(aq)+\ce{3Cl+}(aq)\]

Homme (OH) 2 (s) +HBr (aq) ⟶ ?

Voici un exemple d'hydroxyde métallique réagissant avec un acide où un sel métallique et de l'eau se formeront toujours :

\[Metal Hydroxide + Acid ⟶ Metal Salt + Water\]

Lorsque cette règle est appliquée à cette équation, nous obtenons ce qui suit :

\[\ce{Mn(OH)2}(s)+\ce{HBr}(aq)⟶ \ce{MnBr2}(aq)+\ce{2H2O}(l)\]

Mais pour répondre à cette question, les solutions aqueuses telles que HBr (aq) et MnBr ₂ (aq) peuvent être réécrites comme suit :

\[\ce{Mn(OH)2}(s)+\ce{2H3O+}(aq)+\ce{2Br-}(aq)⟶\ce{Mn2+}(aq)+\ce{2Br-}(aq)+\ce{4H2O}(l)\]

Cr (s) +O ₂ (g) ⟶ ?

Il s'agit de la réaction générale d'un métal réagissant avec l'oxygène qui aboutira toujours à un oxyde métallique. Cependant, l'oxyde métallique est déterminé par l'état d'oxydation du métal, de sorte que cette réaction peut avoir plusieurs résultats, tels que :

\[\ce{4Cr}(s)+\ce{3O2}(g)⟶\ce{2Cr2O3}(s)\]

\[\ce{Cr}(s)+\ce{O2}(g)⟶\ce{2CrO}(s)\]

\[\ce{Cr}(s)+\ce{O2}(g)⟶\ce{CrO2}(s)\]

\[\ce{2Cr}(s)+\ce{3O2}(g)⟶\ce{CrO3}(s)\]

Cependant, le Cr ₂ O ₃ est le principal oxyde de chrome, on peut donc supposer qu'il s'agit du produit général de cette réaction.

Mn ₂ O ₃ (s) +HCl (aq) ⟶ ?

Cela fait suite à la réaction générale d'un oxyde métallique et d'un acide qui aboutira toujours à un sel et à de l'eau.

\[Metal Oxide + Acid ⟶ Salt + Water\]

En utilisant cette réaction générale, similaire aux réactions générales ci-dessus, la réaction se traduira par :

\[\ce{Mn2O3}(s)+\ce{HCl}(aq)⟶\ce{2MnCl3}(s)+\ce{9H2O}(l)\]

Toutefois, comme le HCl est une solution aqueuse, l'équation globale peut également être réécrite comme suit :

\[\ce{Mn2O3}(s)+\ce{6H3O+}(aq)+\ce{6Cl-}(aq)⟶\ce{2MnCl3}(s)+\ce{9H2O}(l)\]

Thé (s) +XSf (₂ g) ⟶ ?

Le titane est capable de réagir avec les halogènes lorsque le titane peut avoir deux états d'oxydation : +3 et +4. Les réactions suivantes suivent chaque état d'oxydation en conséquence :

\[\ce{2Ti}(s)+\ce{3F2}(g)⟶ \ce{2TiF3}(s)\]

\[\ce{Ti}(s)+\ce{2F2}(g)⟶\ce{TiF4}(s)\]

Cependant, comme il existe le symbole « xs », cela indique que du F ₂ est ajouté en excès, de sorte que la deuxième réaction est davantage favorisée car elle mène la réaction à son terme.

GLOBALEMENT :

\[\ce{Ti}(s)+\ce{xsF2}(g)⟶\ce{TiF4}(g)\]

A19.1.17

$\ce{Fe}(s)+\ce{2H3O+}(aq)+\ce{SO4^2-}(aq)⟶\ce{Fe^2+}(aq)+\ce{SO4^2-}(aq)+\ce{H2}(g)+\ce{2H2O}(l)$;
$\ce{FeCl3}(aq)+\ce{3Na+}(aq)+\ce{3OH-}(aq)+\ce{Fe(OH)3}(s)+\ce{3Na+}(aq)+\ce{3Cl+}(aq)$;
$\ce{Mn(OH)2}(s)+\ce{2H3O+}(aq)+\ce{2Br-}(aq)⟶\ce{Mn^2+}(aq)+\ce{2Br-}(aq)+\ce{4H2O}(l)$;
$\ce{4Cr}(s)+\ce{3O2}(g)⟶\ce{2Cr2O3}(s)$;
$\ce{Mn2O3}(s)+\ce{6H3O+}(aq)+\ce{6Cl-}(aq)⟶\ce{2MnCl3}(s)+\ce{9H2O}(l)$;
$\ce{Ti}(s)+xs\ce{F2}(g)⟶\ce{TiF4}(g)$

Q19.1.18

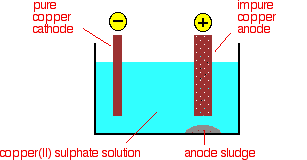
Décrire le procédé électrolytique d'affinage du cuivre.

S19.1.18

Par électrolyse, le cuivre peut être raffiné et purement fabriqué. La raison pour laquelle le cuivre doit éliminer les impuretés est qu'il contribue à augmenter la conductivité électrique des fils électriques. Vous pouvez raffiner le cuivre et éliminer les impuretés par électrolyse. Le cuivre pur est important dans la fabrication des fils électriques, car il crée une meilleure conductivité électrique lors du transfert d'électricité. Pour obtenir une meilleure conductivité électrique, les impuretés doivent être éliminées, ce qui peut être fait en brûlant le cuivre impur pour éliminer les impuretés, telles que le soufre, l'oxygène, etc. et en les transformant en anodes électriques pouvant être utilisées en électrolyse. Les électrodes en cuivre sont ensuite placées dans une cellule électrique (dans des béchers séparés) où le courant électrique peut passer à travers les béchers et atteindre les électrodes. Grâce à ce processus, le cuivre est retiré de l'anode et déposé sur la cathode. Ce processus permet d'éliminer les impuretés et d'affiner le cuivre, car tout le cuivre a été déposé sur la cathode dans une seule électrode. Ce procédé augmente le poids de la cathode en raison du dépôt de cuivre sur la cathode. C'est un excellent exemple de la façon de savoir si une électrode est une cathode ou une anode, comme indiqué dans la question Q17.2.9 ci-dessus.

Résultat de l'image

Q19.1.19

Prédisez les produits des réactions suivantes et équilibrez les équations.

Du Zn est ajouté à une solution de Cr ₂ (SO ₄) ₃ dans un acide.
Du _{FeCl 2} est ajouté à une solution contenant un excès$\ce{Cr2O7^2-}$ d'acide chlorhydrique.
Du Cr ²⁺ est ajouté$\ce{Cr2O7^2-}$ dans une solution acide.
Mn est chauffé avec du CrO ₃.
Du CrO est ajouté au 2HNO ₃ dans l'eau.
Du _{FeCl 3} est ajouté à une solution aqueuse de NaOH.

S19.1.19

est ajouté à une solution d'acide aminé.
- Demi-réaction oxydée : $3Zn(s) \rightarrow 3Zn^{2+}(aq)+6e^-$
- Demi-réaction de réduction : $2Cr^{3+}(aq)+6e^- \rightarrow 2Cr(s)$
- Réaction globale : $Cr_2(SO_4)_3(aq)+2Zn(s)+2H_3O^+(aq)\rightarrow 2Zn^{2+}(aq)+H_2(g)+2H_2O(l)+2Cr^{2+}(aq)+3SO_4^{2-}(aq)$
- Le chrome précipitera hors de la solution car son potentiel de réduction est plus élevé que le zinc ; la réaction est un remplacement unique.
est ajouté à une solution contenant un excès d'acide chlorhydrique.
- Réaction de dissociation : $6FeCl_2(s) \rightarrow 6Fe^{2+}(aq)+12Cl^-(aq)$
- Demi-réaction d'oxydation : $6Fe^{2+}(aq) \rightarrow 6Fe^{3+}(aq)+6e^-$
- Demi-réaction de réduction : $Cr_2O_7^{2-}(aq) + 14 H^+(aq) + 6 e^- \rightarrow 2Cr^{3+}(aq) + 7H_2O(l)$
- Réaction globale : $6FeCl_2(s)+Cr_2O_7^{2-}(aq) + 14 H^+(aq) + 6 e^– \rightarrow 2 Cr^{3+}(aq) + 6Fe^{3+}(aq)+12Cl^-(aq)+7 H_2O(l)$
- Le potentiel de réduction du permanganate étant plus important, la réaction reste favorable même lorsque l'oxydation du permanganate $Fe^{2+}$ est négative.
est ajouté dans une solution acide.
- Demi-réaction de réduction : $Cr_2O_7^{2-}(aq)+14H^+(aq)+6e^- \rightarrow 2Cr^{3+}(aq)+7H_2O(l)$
- Demi-réaction d'oxydation : $6Cr^{2+} \rightarrow 6Cr^{3+}+6e^-$
- Réaction globale : $6Cr^{2+}(aq)+Cr_2O_7^{2-}(aq)+14H^+(aq) \rightarrow 8Cr^{3+}(aq)+7H_2O(l)$
- La réaction est favorable avec un résultat positif élevé $E^\circ$
est chauffé avec.
- Demi-réaction de réduction : $8CrO_3(aq)+24H^++24e^- \rightarrow 4Cr_2O_3(aq)+12H_2O(l)$
- Demi-réaction d'oxydation : $9Mn(s)+12H_2O(l) \rightarrow 3Mn_3O_4(aq)+24H^+(aq)+24e^-$
- Réaction globale : $8CrO_3(aq)+9Mn(s) \rightarrow^{\Delta} 4Cr_2O_3(aq)+3Mn_3O_4(aq)$
- La chaleur crée un produit dont l'énergie est supérieure à celle des deux réactifs précédents.
est ajouté à l'eau.
- Dissociation acide forte : $2HNO_3(aq)+2H_2O(l) \rightarrow 2H_3O^+(aq)+2NO_3^-(aq)$
- Réaction globale : $2HNO_3(aq)+CrO(aq) \rightarrow Cr^{2+}(aq)+2NO_3^-(aq)+H_2O(l)$
- Cette réaction fonctionne par échange d'électrons pour produire des ions chrome.
est ajouté à une solution aqueuse de.
- Réaction globale : $3NaOH(aq)+FeCl_3(s) \rightarrow 3Na^+(aq)+FeOH_3^-(s)+3Cl^-(aq)$
- L'hydroxyde de fer précipitera parce que les deux métaux échangeront des anions.

A19.1.19

$\ce{Cr2(SO4)3}(aq)+\ce{2Zn}(s)+\ce{2H3O+}(aq)⟶\ce{2Zn^2+}(aq)+\ce{H2}(g)+\ce{2H2O}(l)+\ce{2Cr^2+}(aq)+\ce{3SO4^2-}(aq)$;
$\ce{4TiCl3}(s)+\ce{CrO4^2-}(aq)+\ce{8H+}(aq)⟶\ce{4Ti^4+}(aq)+\ce{Cr}(s)+\ce{4H2O}(l)+\ce{12Cl-}(aq)$;
Dans une solution acide entre pH 2 et pH 6,$\ce{CrO4^2-}$ se forme$\ce{HrCO4-}$, qui est en équilibre avec l'ion dichromate. La réaction est$\ce{2HCrO4-}(aq)⟶\ce{Cr2O7^2-}(aq)+\ce{H2O}(l)$. À d'autres pH acides, la réaction est$\ce{3Cr^2+}(aq)+\ce{CrO4^2-}(aq)+\ce{8H3O+}(aq)⟶\ce{4Cr^3+}(aq)+\ce{12H2O}(l)$ :
$\ce{8CrO3}(s)+\ce{9Mn}(s)\overset{Δ}{⟶}\ce{4Cr2O3}(s)+\ce{3Mn3O4}(s)$;
$\ce{CrO}(s)+\ce{2H3O+}(aq)+\ce{2NO3-}(aq)⟶\ce{Cr^2+}(aq)+\ce{2NO3-}(aq)+\ce{3H2O}(l)$;
$\ce{CrCl3}(s)+\ce{3NaOH}(aq)⟶\ce{Cr(OH)3}(s)+\ce{3Na+}(aq)+\ce{3Cl-}(aq)$

Q19.1.20

Quel est le gaz produit lorsque le sulfure de fer (II) est traité avec un acide non oxydant ?

S19.1.20

Formule pour le sulfure de fer (II) :\[FeS\]

Définition de l'acide non oxydant : Un acide non oxydant est un acide qui n'agit pas comme agent oxydant. Son anion est un agent oxydant plus faible que le H+, il ne peut donc pas être réduit. Exemples d'acides non oxydants :\[HCl, HI, HBr, H_3PO_4, H_2SO_4\]

Étape 2 : Choisissez l'un des acides non oxydants, dans ce cas HCl, et écrivez la réaction chimique :

\[FeS(s)+2HCl(aq)\rightarrow FeCl_2(s)+H_2S(g)\]

Le gaz produit lorsque le sulfure de fer (II) est traité avec un acide non oxydant, le HCl, est du H ₂ S (sulfure de dihydrogène) gazeux.

Q19.1.21

Prédisez les produits de chacune des réactions suivantes, puis équilibrez les équations chimiques.

Le Fe est chauffé dans une atmosphère de vapeur.
Du NaOH est ajouté à une solution de Fe (NO ₃) ₃.
Du FeSO ₄ est ajouté à une solution acide de KmNO ₄.
Du Fe est ajouté à une solution diluée de H ₂ SO ₄.
Une solution de Fe (NO ₃) ₂ et de HNO ₃ est laissée à l'air.
Du FeCO ₃ est ajouté à une solution de HClO ₄.
Le Fe est chauffé à l'air.

S19.1.21

a. La vapeur c'est de l'eau ($\ce{H_{2}O}$)

Nous pouvons écrire la réaction comme suit :

$\ce{Fe}$+$\ce{H_{2}O}$ → ?

Il s'agit d'une réaction de remplacement unique, donc$\ce{Fe}$ remplace$\ce{H_{2}}$. Ainsi, l'un des produits est qu'$\ce{Fe_{3}O_{4}}$il s'agit d'une combinaison d'oxyde de fer (II) et d'oxyde de fer (III)$\ce{Fe_{2}O_{3}}$.$\ce{FeO}$

$\ce{Fe}$Il est chauffé dans une atmosphère de vapeur. $\ce{H_{2}}$se charge de manière neutre et devient un autre produit.

Après avoir équilibré les coefficients, la réaction finale est la suivante :

$\ce{3Fe}(s)$+$\ce{4H_{2}O}(g)$ →$\ce{Fe_{3}O_{4}}(s)$ +$\ce{4H_{2}}(g)$

b.$\ce{NaOH}$ ajouté à une solution de$\ce{Fe(NO_{3})_{3}}$ est une double réaction de remplacement et de précipitation.

Nous pouvons écrire la réaction comme suit :

$\ce{NaOH}$+$\ce{Fe(NO_{3})_{3}}$ → ?

Le$\ce{Na}$ et$\ce{Fe}$ passe à la forme$\ce{Fe(OH)_{3}}(s)$ et$\ce{NaNO_{3}}(aq)$.

$\ce{Fe(OH)_{3}}$est solide car insoluble selon les règles de solubilité.

Après avoir équilibré les coefficients de la réaction, la réaction finale est la suivante :

$\ce{Fe(NO_{3})_{3}}(aq)$+$\ce{3NaOH}(aq)$ →$\ce{Fe(OH)_{3}}(s)$ +$\ce{NaNO_{3}}(aq)$

c. Par exemple, l'acide utilisé pour fabriquer la solution acide est$\ce{H_{2}SO_{4}}$, alors la réaction est :

$\ce{FeSO_{4}}$+$\ce{KMnO_{4}}$ +$\ce{H_{2}SO_{4}}$ →$\ce{Fe_{2}(SO_{4})_{3}}$ +$\ce{MnSO_{4}}$ +$\ce{H_{2}O}$ +$\ce{K_{2}SO_{4}}$

Ensuite, la réaction ionique nette doit être écrite pour éliminer les ions spectateurs présents dans la réaction, cela s'écrit comme suit :

$\ce{Fe^{2+}}$+$\ce{MnO_{4}^{-}}$ +$\ce{H^{+}}$ →$\ce{Fe^{3+}}$ +$\ce{Mn^{2+}}$ +$\ce{H_{2}O}$

Comme le montre l'équation ionique nette ci-dessus,$\ce{Fe^{2+}}$ est oxydé$\ce{Fe^{3+}}$ et$\ce{MnO_{4}^{-}}$ réduit à$\ce{Mn^{2+}}$. Elles peuvent être écrites sous la forme de deux demi-réactions :

$\ce{Fe^{2+}}$→$\ce{Fe^{3+}}$

$\ce{MnO_{4}^{-}}$→$\ce{Mn^{2+}}$

Pour équilibrer la demi-réaction d'oxydation, un électron doit être ajouté à la$\ce{Fe^{3+}}$, comme suit :

$\ce{Fe^{2+}}$→$\ce{Fe^{3+}}$ +$\ce{e^{-}}$

La demi-réaction de réduction doit également être équilibrée, mais avec$\ce{H^{+}}$ des ions$\ce{H_{2}O}$, ce qui se traduit par :

$\ce{MnO_{4}^{-}}$+$\ce{8H^{+}}$ →$\ce{Mn^{2+}}$ +$\ce{4H_{2}O}$

Une fois la charge des$\ce{Mn}$ atomes équilibrée, la charge globale doit être équilibrée des deux côtés, car du côté des réactifs, la charge est$\ce{7+}$ et la charge du côté des produits l'est$\ce{2+}$. La charge globale peut être équilibrée en ajoutant des électrons, comme suit :

$\ce{MnO_{4}^{-}}$+$\ce{8H^{+}}$ +$\ce{5e^{-}}$ →$\ce{Mn^{2+}}$ +$\ce{4H_{2}O}$

Maintenant que les deux demi-réactions sont équilibrées, les électrons des deux demi-réactions doivent être égaux, puis les demi-réactions sont additionnées. Une fois cela fait, la réaction ressemble à ceci :

$\ce{MnO_{4}^{-}}$+$\ce{8H^{+}}$ +$\ce{5Fe^{2+}}$ +$\ce{5e^{-}}$ →$\ce{Mn^{2+}}$ +$\ce{4H_{2}O}$ +$\ce{5Fe^{3+}}$ +$\ce{5e^{-}}$

Les deux$\ce{5e^{-}}$ côtés s'annulent et la réaction finale équilibrée est la suivante :

$\ce{MnO_{4}^{-}}$+$\ce{8H^{+}}$ +$\ce{5Fe^{2+}}$ →$\ce{Mn^{2+}}$ +$\ce{4H_{2}O}$ +$\ce{5Fe^{3+}}$

d.$\ce{Fe}$ ajouté à une solution diluée de$\ce{H_{2}SO_{4}}$ est une seule réaction de remplacement.

Le$\ce{Fe}$ est ajouté à une solution diluée de manière à ce qu'$\ce{H_{2}SO_{4}}$il soit écrit sous forme d'ions séparés.

Nous pouvons écrire la réaction comme suit :

$\ce{Fe}(s)$+$\ce{2H^+}(aq)$ +$\ce{(SO_{4})^{2-}}(aq)$ → ?

Le Fe remplace l'$\ce{H^+}$ion et devient un$\ce{Fe^{2+}}$ ion.

$\ce{H_{2}O}$est également un produit car la solution est diluée.

En outre, il doit$\ce{FeSO_{4}}$ également être séparé en ions à la$\ce{Fe}$ suite de son ajout à une solution diluée.

Après avoir équilibré tous les coefficients, la réaction finale est la suivante :

$\ce{Fe}(s)$+$\ce{(2H_{3}O)^+}(aq)$ +$\ce{(SO_{4})^{2-}}(aq)$ →$\ce{Fe^{2+}}(aq)$ +$\ce{SO_{4}^{2-}}(aq)$ +$\ce{H_{2}}(g)$ +$\ce{2H_{2}O}(l)$

Remarque :$\ce{H^+}$ peut également être écrit comme l'ion hydronium,$\ce{(H_{3}O)^{+}}$.

e. Dans un premier temps, nous pouvons écrire :

$\ce{4Fe(NO_{3})_{2}}$+$\ce{4HNO_{3}}$ +$\ce{O_{2}}$ → ?

Nous écrivons le terme oxygène dans les réactifs car il est indiqué que la solution peut rester dans l'air.

Il suffit d'analyser les produits possibles qui peuvent se former et nous pouvons voir que l'hydrogène de l'acide nitrique peut se combiner avec de l'oxygène gazeux pour former de l'eau, puis en combinant le tout, nous obtenons la réaction finale suivante :

$\ce{4Fe(NO_{3})_{2}}(aq)$+$\ce{4HNO_{3}}(aq)$ +$\ce{O_{2}}(g)$ →$\ce{2H_{2}O}(l)$ +$\ce{4Fe(NO_{3})_{3}}(aq)$

f. Lorsqu'il$\ce{FeCO_{3}}$ est ajouté$\ce{HClO_{4}}$, une double réaction de remplacement se produit.

L'$\ce{Fe^{2+}}$ion change de points avec l'$\ce{H^+}$ion pour se former$\ce{Fe(ClO_{4})_{2}}$ sous forme de produit.

Lorsque l'$\ce{H^+}$ion est ajouté à l'$\ce{(CO_{3})^{2-}}$ion,$\ce{H_{2}CO_{3}}$ il se forme.

Après avoir équilibré les coefficients, la réaction finale est la suivante :

$\ce{FeCO_{3}}(s)$+$\ce{HClO_{4}}(aq)$ →$\ce{Fe(ClO_{4})_{2}}(aq)$ +$\ce{H_{2}O}(l)$ +$\ce{CO_{2}}(g)$

g. L'air est composé d'oxygène gazeux, qui est une molécule diatomique, il en est ainsi$\ce{O_{2}}$.

L'ajout$\ce{Fe}$ de à$\ce{O_{2}}$ provoquera la formation d'une réaction de synthèse$\ce{Fe_{2}O_{3}}$.

Après équilibrage des coefficients, la réaction finale est la suivante :

$\ce{3Fe}(s)$+$\ce{2O_{2}}(g)$ →$\ce{Fe_{2}O_{3}}(s)$

A19.1.21

$\ce{3Fe}(s)+\ce{4H2O}(g)⟶\ce{Fe3O4}(s)+\ce{4H2}(g)$;
$\ce{3NaOH}(aq)+\ce{Fe(NO3)3}(aq)\xrightarrow{\ce{H2O}}\ce{Fe(OH)3}(s)+\ce{3Na+}(aq)+\ce{3NO3-}(aq)$;
$\ce{MnO_{4}^{-}}$+$\ce{8H^{+}}$ +$\ce{5Fe^{2+}}$ →$\ce{Mn^{2+}}$ +$\ce{4H_{2}O}$ +$\ce{5Fe^{3+}}$
$\ce{Fe}(s)$+$\ce{(2H_{3}O)^+}(aq)$ +$\ce{(SO_{4})^{2-}}(aq)$ →$\ce{Fe^{2+}}(aq)$ +$\ce{SO_{4}^{2-}}(aq)$ +$\ce{H_{2}}(g)$ +$\ce{2H_{2}O}(l)$
$\ce{4Fe(NO_{3})_{2}}(aq)$+$\ce{4HNO_{3}}(aq)$ +$\ce{O_{2}}(g)$ →$\ce{2H_{2}O}(l)$ +$\ce{4Fe(NO_{3})_{3}}(aq)$
$\ce{FeCO_{3}}(s)$+$\ce{HClO_{4}}(aq)$ →$\ce{Fe(ClO_{4})_{2}}(aq)$ +$\ce{H_{2}O}(l)$ +$\ce{CO_{2}}(g)$
$\ce{3Fe}(s)$+$\ce{2O_{2}}(g)$ →$\ce{Fe_{2}O_{3}}(s)$

Q19.1.22

Équilibrez les équations suivantes par des méthodes d'oxydoréduction ; notez que trois éléments changent d'état d'oxydation.

\[\ce{Co(NO3)2}(s)⟶\ce{Co2O3}(s)+\ce{NO2}(g)+\ce{O2}(g)\]

S19.1.22

Équilibrez les équations suivantes par des méthodes d'oxydoréduction ; notez que trois éléments changent d'état d'oxydation.

\[Co(NO_3){_2(s)}⟶Co_2O{_3(s)}+NO{_2(g)}+O{_2(g)}\]

Dans cette réaction, N change les états d'oxydation de +5 à +4 (réduit), le Co change les états d'oxydation de +2 à +3 (oxydé) et O change les états d'oxydation de -2 à 0 (également oxydé).

Tout d'abord, divisez cette réaction en un demi-ensemble de réactions d'oxydation et de réduction, et équilibrez tous les éléments qui ne sont ni de l'hydrogène ni de l'oxygène (nous y reviendrons plus tard) :

\[Reduction: 2Co(NO_3){_2}\rightarrow Co_2O_{3}+4NO_2\]

Maintenant, en ce qui concerne la réaction d'oxydation, nous ne traitons que de l'O ₂ côté des produits. Pour équilibrer cela, nous devrons ajouter de l'eau et de l'hydrogène des deux côtés :

\[Oxidation: 2H_2O\rightarrow O_2+4H^+ \]

Équilibrez la quantité d'oxygène de chaque côté en ajoutant le nombre correct de molécules d'eau (H ₂ O) et équilibrez la quantité d'hydrogène en ajoutant le nombre correct d'atomes ^H+ :

\[Reduction: 2H^++2Co(NO_3){_2}\rightarrow Co_2O_{3}+4NO_2+H_2O\]

\[Oxidation: 2H_2O\rightarrow O_2+4H^+\]

Enfin, équilibrez les charges en ajoutant des électrons de chaque côté de l'équation. Pour la réaction de réduction, nous ajouterons 2 électrons pour équilibrer le 2H ⁺, et à la réaction d'oxydation, nous ajouterons 4 électrons pour équilibrer le ^4H+. N'oubliez pas que le but de cette étape est de s'assurer que les charges sont équilibrées, afin que nous puissions les annuler à la fin.

\[Reduction: 2e^- + 2H^++2Co(NO_3){_2}\rightarrow Co_2O_{3}+4NO_2+H_2O\]

\[Oxidation: 2H_2O\rightarrow O_2+4H^+ +4e^-\]

Multipliez la réaction de réduction par deux, afin d'équilibrer les charges de manière à ce qu'il y ait 4 électrons de chaque côté de la réaction.

\[Reduction: 2(2e^- + 2H^++2Co(NO_3){_2}\rightarrow Co_2O_{3}+4NO_2+H_2O)\]

et combinez les deux réactions qui se traduisent par :

\[2H_2O + 4Co(NO_3)_2 + 4H^+ \rightarrow 2CO_2O_3 + 8NO_2 + 2H_2O + O_2 + 4H^+\]

Annulez les termes similaires :

\[4Co(NO_3){_2(s)} \rightarrow 2CO_2O{_3(s)} + 8NO{_2(g)} + O{_2(g)}\]

Les deux côtés ont des charges globales de 0 et peuvent être vérifiées pour voir si elles sont équilibrées.

A19.1.22

\[4Co(NO_3){_2(s)} \rightarrow 2CO_2O{_3(s)} + 8NO{_2(g)} + O{_2(g)}\]

Q19.1.23

La solution diluée de cyanure de sodium est lentement versée dans une solution de nitrate d'argent lentement agitée. Un précipité blanc se forme temporairement mais se dissout lorsque l'ajout de cyanure de sodium se poursuit. Utilisez des équations chimiques pour expliquer cette observation. La solubilité du cyanure d'argent est similaire au chlorure d'argent.

S19.1.23

R : Étape 1 : examinez la question et commencez à écrire une formule générale entre le produit et le réactif pour cette réaction.

Étape 2 : essayez de comprendre pourquoi un précipité se forme, mais seulement pendant une période limitée, avant de le reformer dans une substance aqueuse.

Étape 3 : À l'étape 2, vous devriez avoir remarqué que la réaction est une réaction en plusieurs étapes et, en utilisant la formule approximative que vous avez dérivée à l'étape 1, vous devriez essayer de voir quelle est la série d'étapes qui mènent au produit global d'AgCN ₂ liquide.

Dans cette réaction, nous voyons comment le NaCN est ajouté à l'AgNO ₃. Un précipité se forme puis disparaît avec l'ajout d'encore plus de NaCN, ce qui doit signifier qu'il s'agit d'une réaction intermédiaire qui n'apparaîtra pas comme le produit final. L'argent et le cyanure se lient temporairement, mais la liaison étant trop faible pour les maintenir ensemble, ils se séparent à nouveau lorsque du NaCN est ajouté, car un nouveau composé plus résistant et plus stable se forme : [Ag (CN) ₂] ^- (aq).

L'équation réelle de la réaction lorsqu'elle se produit pour la première fois est\[AgCl(aq)+NaCN(aq)\rightarrow AgCN(s)+NaCl(aq)\]

Cela peut être écrit de la manière suivante : à mesure que l'on ajoute du CN ⁻, l'argent et le cyanure se combinent : Ag ⁺ (aq) +CN ⁻ (aq) →AgCN (s)

^{Au fur et à mesure que l'on ajoute du CN, l'argent et deux cyanures se combinent pour créer un composé plus stable : Ag ⁺ (aq) +2CN ⁻ (aq) → [Ag (CN) ₂] ^- (aq)}

AgCN (s) + CN ^- (aq) → [AgC (CN) ₂] ^- (aq)

A19.1.23

Lorsque CN ⁻ est ajouté,

\[\ce{Ag+}(aq)+\ce{CN-}(aq)⟶\ce{AgCN}(s)\]

Au fur et à mesure que CN ⁻ est ajouté,

\[\ce{Ag+}(aq)+\ce{2CN-}(aq)⟶\ce{[Ag(CN)2]-}(aq)\]

\[\ce{AgCN}(s)+\ce{CN-}(aq)⟶\ce{[Ag(CN)2]-}(aq)\]

Q19.1.24

Prédisez lequel sera le plus stable, [CrO ₄] ²⁻ ou [WO ₄] ²⁻, et expliquez.

S19.1.24

Selon les règles associées aux énergies de stabilisation du champ cristallin, les molécules stables contiennent plus d'électrons dans les orbitales moléculaires de basse énergie que dans les orbitales moléculaires de haute énergie. Dans ce cas, les deux complexes ont du O ₄ comme ligands et ont tous deux une charge -2. Par conséquent, vous déterminez la stabilité en comparant les métaux. Le chrome se trouve dans la 3e orbitale, selon le tableau périodique. Le tungstène (W) se trouve sur l'orbitale 5d. 3d est un niveau d'énergie inférieur à celui de la 5D. Les orbitales de niveau supérieur sont plus facilement ionisées et rendent leur forme élémentaire de base plus stable. Si la forme élémentaire est plus stable, la forme oxydée est moins stable. Par conséquent, le [CrO ₄] ²⁻ est plus stable que le [WO ₄] ²⁻.

A19.1.24

[CrO ₄] ^2- est plus stable car le chrome se trouve sur l'orbite 3D tandis que le tungstène se trouve sur l'orbitale 4d, ce qui a un niveau d'énergie plus élevé et le rend moins stable.

Q19.1.25

Indiquer l'état d'oxydation du métal pour chacun des oxydes suivants de la première série de transition. (Conseil : Les oxydes de formule M ₃ O ₄ sont des exemples de composés à valence mixte dans lesquels l'ion métallique est présent dans plus d'un état d'oxydation. Il est possible d'écrire ces formules composées dans le format équivalent MO·M ₂ O ₃, afin de permettre l'estimation des deux états d'oxydation du métal.)

Sc ₂ O ₃
TiO ₂
V ₂ DE ₅
CrO ₃
N° ₂
₃ ou ₄ févr.
Co ₃ O ₄
Non
_{Tasse 2} L

S19.1.25

La première étape pour résoudre ce problème consiste à examiner les règles des états oxydants pour divers éléments :

chem.libretexts.org/Core/Analytical_Chemistry/Electrochimie/Redox_Chemistry/Oxidation_State

Les principales règles qui seront utilisées pour résoudre ces problèmes seront la règle 6 relative à l'état d'oxydation, selon laquelle l'état d'oxydation de l'oxygène est (-2), et la règle 2, selon laquelle la somme totale de l'état d'oxydation de tous les atomes d'une espèce donnée est égale à la charge nette de cette espèce. La résolution de ces problèmes nécessite une algèbre simple. Les états d'oxydation des deux éléments du composé étant égaux à zéro, définissez l'oxydation inconnue de l'élément qui n'est pas de l'oxygène sur une variable${x}$ et l'état d'oxydation de l'oxygène égal à${-2}$. Multipliez ensuite les deux états d'oxygène par le nombre d'atomes de l'élément présent. Additionnez les valeurs, définissez l'équation à zéro et résolvez pour${x}$.

$\ce{Sc2O3}={3{(-2)}}+{2{x}}={0}⟶{-6}+{2{x}}={0}⟶{x}={Sc}={+3}$$Sc^{3+}$
$\ce{TiO2}={2{(-2)}}+{x}={0}⟶{-4}+{x}={0}⟶{x}={Ti}={+4}$$Ti^{4+}$
$\ce{V2O5}={5{(-2)}}+{2{x}}={0}⟶{-10}+{2{x}}={0}⟶{x}={V}={+5}$$V^{5+}$
$\ce{CrO3}={3{(-2)}}+{x}={0}⟶{-6}+{x}={0}⟶{x}={Cr}={+6}$$Cr^{6+}$
$\ce{MnO2}={2{(-2)}}+{x}={0}⟶{-4}+{x}={0}⟶{x}={Mn}={+4}$$Mn^{4+}$
$\ce{Fe3O4}=\ce{FeO}·\ce{Fe2O3}=$

$\ce{FeO}={-2}+{x}={0}⟶{x}={Fe}={+2}$$Fe^{2+}$

$\ce{Fe2O3}={3{(-2)}}+{2{x}}={0}⟶{-6}+{2x}={0}⟶{x}={Fe}={+3}$$Fe^{3=}$

(Un atome de Fe a un état d'oxydation de +2 et les 2 autres atomes de Fe ont un état d'oxydation de +3)

7. $\ce{Co3O4}=\ce{CoO}·\ce{Co2O3}=$

$\ce{CoO}={-2}+{x}={0}⟶{x}={Co}={+2}$$Co^{2+}$

$\ce{Co2O3}={3{(-2)}}+{2{x}}={0}⟶{-6}+{2x}={0}⟶{x}={Co}={+3}$$Co^{3+}$

(Un atome de Co a un état d'oxydation de +2 et les 2 autres atomes de Co ont un état d'oxydation de +3)

8. $\ce{NiO}={-2}+{x}={0}⟶{x}={Ni}={+2}$$Ni^{2+}$

9. $\ce{Cu2O}={-2}+{2{x}}={0}⟶{-2}+{2x}={0}⟶{x}={Cu}={+1}$$Cu^{1+}$

A19.1.25

Sc ³⁺ ; Ti ⁴⁺ ; V ⁵⁺ ; Cr ⁶⁺ ; Mn ⁴⁺ ; Fe ²⁺ et Fe ³⁺ ; Co ²⁺ et Co ³⁺ ; Ni ²⁺ ; Cu ⁺

19.2 : Chimie de coordination des métaux de transition

Q19.2.1

Indiquez le numéro de coordination de l'atome métallique central dans chacun des composés de coordination suivants :

[Pt (H ₂ O) ₂ Br ₂]
[Pt (NH ₃) (py) (Cl) (Br)] (py = pyridine, C ₅ H ₅ N)
[Zn (NH ₃) ₂ Cl ₂]
[Zn (NH ₃) (py) (Cl) (Br)]
[Ni (H ₂ O) ₄ Cl ₂]
[Fe (en) ₂ (CN) ₂] ⁺ (fr = éthylènediamine, C ₂ H ₈ N ₂)

ARTICLE 19.2.1

Nous devons d'abord déterminer si le ligand possède plus d'un atome lié (bidentate/polydentate). En utilisant le tableau ci-dessous, nous sommes en mesure de le faire.

Ligand	Nombre d'atomes liés
Ammine (NH ₃)	monodentate
Eau (H ₂ O)	monodentate
Bromö (Br)	monodentate
Chloro (Cl)	monodentate
Cyano (NC)	monodentate
Pyridine (C ₅ H ₅ N)	monodentate
Éthylènediamine (C ₂ H ₈ N ₂)	bidenté

Maintenant que nous avons identifié le nombre d'atomes liés à chaque ligand, nous pouvons trouver le nombre total d'atomes liés à l'ion métallique central, ce qui nous donne le numéro de coordination.

$[Pt(H_2O)_2Br_2]$: Nous pouvons identifier l'ion métallique du complexe comme étant le Pt, le platine, car les deux autres sont répertoriés comme ligands ci-dessus et ne sont pas métalliques. Nous pouvons maintenant utiliser le nombre de ligands et leurs atomes de liaison pour trouver son numéro de coordination. Le tableau ci-dessus montre que H ₂ O ne possède qu'un seul atome de liaison, ainsi que du Br. Ainsi, pour chaque atome de Br, nous avons un atome de liaison, et nous en avons deux, produisant 2 atomes de liaison ; il en va de même pour H ₂ O, ce qui nous donne un nombre total de 4 atomes de liaison, et donc un nombre de coordination de 4.
$[Pt(NH_3)(py)(Cl)(Br)]$(py = pyridine, C ₅ H ₅ N) : L'ion métallique de ce complexe, similaire au premier, peut être identifié comme étant Pt, platine. Les ligands peuvent être identifiés comme NH ₃, pyridine, Cl et Br, qui sont tous des ligands monodentés et possèdent chacun un atome de liaison. Comme nous avons quatre ligands, chacun ayant un atome de liaison, le nombre total d'atomes de liaison sur l'ion métallique est de 4, donc le complexe a un numéro de coordination de 4.
$[Zn(NH_3)_2Cl_2]$: L'ion métallique de ce complexe peut être identifié comme Zn, zinc, et les ligands peuvent être identifiés comme NH ₃ et Cl. Comme ces deux sont tous deux des ligands monodentés, ils ont chacun un atome de liaison. Comme nous avons un total de deux ligands NH ₃ et de deux ligands Cl, nous obtenons un total de quatre ligands monodentés, ce qui nous donne 4 atomes de liaison et un nombre de coordination de 4.
$[Zn(NH_3)(py)(Cl)(Br)]$: L'ion métallique de ce complexe peut être identifié comme Zn, zinc, et les ligands peuvent être identifiés comme NH ₃, pyridine, Cl et Br, qui sont tous des ligands monodentés et possèdent chacun un atome de liaison. Comme nous avons quatre ligands, chacun ayant un atome de liaison, le nombre total d'atomes de liaison sur l'ion métallique est de 4, donc le complexe a un numéro de coordination de 4.
$[Ni(H_2O)_4Cl_2]$: L'ion métallique de ce complexe peut être identifié comme étant Ni, nickel, et nous pouvons maintenant utiliser le nombre de ligands et leurs atomes de liaison pour trouver son numéro de coordination. Le tableau ci-dessus montre que H ₂ O ne possède qu'un seul atome de liaison, ainsi que du Cl. Ainsi, pour chaque atome de Cl, nous avons un atome de liaison, et nous en avons deux, ce qui donne 2 atomes de liaison. H ₂ O est identique, n'ayant qu'un seul atome de liaison, mais il y en a quatre. Cela nous donne donc un nombre total de 6 atomes de liaison, et donc un nombre de coordination de 6.
$[Fe(en)_2(CN)_2]^+$(en = éthylènediamine, C ₂ H ₈ N ₂) : L'ion métallique de ce complexe peut être identifié comme étant Fe, fer, et les ligands peuvent être identifiés comme (en) et CN. Puisque (en) est bidenté, c'est-à-dire qu'il possède 2 atomes de liaison, et qu'il y en a deux, le nombre total d'atomes de liaison provenant de (en) est de quatre. Puisque le CN est monodentate, c'est-à-dire qu'il possède un atome de liaison, et qu'il y en a deux, le nombre total d'atomes de liaison du ligand CN est de deux. Ainsi, le nombre total d'atomes de liaison est de 6, donc le complexe a un nombre de coordination de 6.

A19.2.1

Les 2 ligands aqua et les 2 ligands bromo forment un total de 4 liaisons covalentes coordonnées et, par conséquent, le nombre de coordination est de 4.
L'amine, la pyridine, le chloro et le brome forment chacun une liaison covalente coordonnée qui donne un total de 4 et donc CN=4.
Deux ligands amines et deux ligands chlorés donnent un total de 4 liaisons covalentes coordonnées et un CN = 4.
Un ligand amine, une pyrimidine, un chloro et un brome forment un total de 4 liaisons covalentes, ce qui donne CN = 4.
Quatre ligands aquatiques et deux ligands chlorés forment un total de 6 liaisons covalentes coordonnées et un CN = 6.
L'éthylènediamine est un ligand bidenté qui forme deux liaisons covalentes coordonnées ; avec deux ligands cyano, elle forme un total de 6 liaisons et possède donc un CN = 6.

Q19.2.2

Donnez les numéros de coordination et écrivez les formules pour chacun des éléments suivants, y compris tous les isomères, le cas échéant :

ion tétrahydroxozincate (II) (tétraédrique)
ion hexacyanopalladate (IV)
ion dichloroaurate (notez que aurum signifie « or » en latin)
diamminedichloroplatine (II)
diamminettétrachlorochromate de potassium (III)
hexaamminecobalt (III) hexacyanochromate (III)
nitrate de dibromobis (éthylènediamine) cobalt (III)

ARTICLE 19.2.2

Pour déterminer les nombres de coordination, nous devons compter le nombre total de ligands liés au métal central et distinguer les ligands monodentés des ligands polydentés. Pour déterminer les formules, nous utilisons les règles de nomenclature et travaillons à rebours.

« tétrahydroxo » = 4 ligands hydroxydes ; comme l'hydroxyde est un ligand monodentate, nous avons un total de 4 liaisons avec le métal central.
Numéro de coordination : 4
Nous passons en revue les bases de la nomenclature et voyons que « tetra » = 4 et « hydroxo » = OH ^-. Puisque la charge sur le zinc est de 2+, ce qui est donné dans la nomenclature par des chiffres romains, nous pouvons calculer que la charge totale sur le complexe est de 2-.
Formule : [Zn (OH) ₄] ²⁻
« hexacyano » = 6 ligands cyanurés ; le cyanure étant un ligand monodenté, nous avons un total de 6 liaisons avec le métal central.
Numéro de coordination : 6
Nous passons en revue les bases de la nomenclature et voyons que « hexa » = 6 et « cyano » = CN ^-. Puisque la charge sur le Pd est de 4+, ce qui est donné dans la nomenclature par des chiffres romains, nous pouvons calculer que la charge totale sur le complexe est de 2-.
Formule : [Pd (CN) ₆] ²⁻
« dichloro » = 2 ligands chlorés ; comme le chlorure est un ligand monodentate, nous avons un total de 2 liaisons avec le métal central.
Numéro de coordination : 2
Nous passons en revue les bases de la nomenclature et voyons que « di » = 2 et « chloro » = Cl ^-. Comme la charge sur Au est toujours de 1+, nous pouvons calculer la charge totale sur le complexe à 1-.
Formule : [AuCl ₂] ⁻
« diammine » = 2 ligands ammoniacaux et « dichloro » = 2 ligands chlorures ; comme les ligands ammoniacaux et chlorures sont tous deux monodentés, nous avons un total de 4 liaisons avec le métal central.
Numéro de coordination : 4
Nous passons en revue les bases de la nomenclature et voyons que « di » = 2, « chloro » = Cl ^- et « ammine » = NH ₃. Puisque la charge sur Pt est de 2+, ce qui est donné dans la nomenclature par les chiffres romains, nous pouvons calculer que la charge totale est de 0, donc le complexe est neutre.
Formule : [Pt (NH ₃) ₂ Cl ₂]
« diammine » = 2 ligands ammoniacaux et « tétrachloro » = 4 ligands chlorures ; comme les ligands ammoniacaux et chlorures sont tous deux monodentés, nous avons un total de 6 liaisons avec le métal central.
Numéro de coordination : 6
Nous passons en revue les bases de la nomenclature et voyons que « di » = 2, « ammine » = NH ₃, « tetra » = 4 et « chloro » = Cl ^-. Puisque la charge sur le métal central, Cr, est de 3+, ce qui est donné dans la nomenclature par des chiffres romains, nous pouvons calculer que la charge totale du complexe est de 1-. Le « potassium » au début de la nomenclature indique qu'il s'agit du cation correspondant à ce complexe anionique.
Formule : K [Cr (NH ₃) ₂ Cl ₄]
Les deux complexes métalliques possèdent des ligands monodentates « hexa », ce qui signifie que les deux ont des numéros de coordination de 6.
Numéro de coordination : 6
Nous passons en revue les bases de la nomenclature et voyons que « hexa » = 6, « ammine » = NH ₃ et « cyano » = CN ^-. Puisque la charge sur Cr est de 3+ et que Co est de 3+, ce qui est donné dans la nomenclature par des chiffres romains, nous constatons que les charges de ces complexes s'équilibrent.
Formule : [Co (NH ₃) ₆] [Cr (CN) ₆]
« dibromo » = 2 ligands bromures « bis (éthylènediamine) » = 2 ligands (en) ; le bromure est un ligand monodentate tandis que (en) est un ligand bidenté. Par conséquent, nous avons un numéro de coordination de 6.
Numéro de coordination : 6
Nous passons en revue les bases de la nomenclature et voyons que « di » = 2, « bromo » = Br ^-, « bis » = 2 et « éthylènediamine » = en. Puisque la charge sur le Co est de 3+, ce qui est donné dans la nomenclature par les chiffres romains, nous constatons que la charge totale du complexe est de 1+. Le nitrate est l'anion correspondant à ce complexe cationique.
Formule : [Co (en) ₂ Br ₂] NO ₃

A19.2.2

4, [Zn (OH) ₄] ²⁻ ;
6, [Pd (CN) ₆] ²⁻ ;
2, [UCl ₂] ⁻ ;
4, [Pt (NH ₃) ₂ Cl ₂] ;
6, K [Cr (NH ₃) ₂ Cl ₄] ;
6, [Co (NH ₃) ₆] [Cr (CN) ₆] ;
6, [Co (fr) ₂ Br ₂] NO ₃

Q19.2.3

Donnez le numéro de coordination pour chaque ion métallique dans les composés suivants :

[Co (CO ₃) ₃] ³⁻ (notez que le CO ₃ ²⁻ est bidenté dans ce complexe)
[Cu (NH ₃) ₄] ²⁺
[Co (NH ₃) ₄ Br _₂] (SO ₄) ₃
[Pt (NH ₃) ₄] [PtCl ₄]
[Cr (fr) ₃] (NO ₃) ₃
[Pd (NH ₃) ₂ Br ₂] (plan carré)
K ₃ [Cu (Cl) ₅]
[Zn (NH ₃) ₂ Cl ₂]

ARTICLE 19.2.3

Vous pouvez déterminer le numéro de coordination d'un composé en fonction du nombre de ligands liés à l'atome central.

1) Dans ce composé, le cobalt est l'atome central et 3 molécules de CO ₃ ^2- y sont attachées. Cependant, le CO ₃ ^2- est un ligand bidenté, ce qui signifie qu'il se lie à l'atome central à deux endroits plutôt qu'à un. Cela signifie que le numéro de coordination de [Co (CO ₃) ₃] ^3- est 6. Un numéro de coordination de 6 signifie que la structure est très probablement octaédrique.

2) Dans ce composé, le cuivre est l'atome central. 4 molécules d'ammoniac y sont attachées. Cela signifie que le numéro de coordination est 4 et que la structure est probablement tétraédrique.

3) Pour ce composé, on peut ignorer le (SO ₄) ₃ car il n'est pas lié à l'atome central. L'atome central est le cobalt, auquel sont liées 4 molécules d'ammoniac et 2 molécules de brome. Le numéro de coordination est 6.

4) Il y a deux composés ici, indiqués par les parenthèses. L'atome central des deux est le platine. L'une d'elles possède 4 molécules d'ammoniac attachées et l'autre 4 atomes de chlore attachés. Les deux complexes ont un numéro de coordination de 4.

5) Nous pouvons ignorer (NO ₃) ₃ pour ce composé. L'atome central est le chrome. Trois molécules d'éthylènediamine sont fixées au chrome. L'éthylènediamine est un ligand bidenté, donc le numéro de coordination est 6.

6) Le palladium est l'atome central. 2 molécules d'ammoniac et 2 atomes de brome sont liés à l'atome de palladium. Le numéro de coordination est 4.

7) Nous pouvons ignorer la structure K ₃. Le cuivre est l'atome central et 5 molécules de chlore y sont attachées. Le numéro de coordination est 5, de sorte que la structure est soit trigonale bipyramidale, soit pyramidale carrée.

8) Dans ce composé, le zinc est l'atome central. Deux molécules d'ammoniac et deux atomes de chlore y sont attachés. Cela signifie que le numéro de coordination est 4.

Q19.2.4

Esquissez les structures des complexes suivants. Indiquez tous les isomères cis, trans et optiques.

[Pt (H ₂ O) ₂ Br ₂] (plan carré)
[Pt (NH ₃) (py) (Cl) (Br)] (plan carré, py = pyridine, C ₅ H ₅ N)
[Zn (NH ₃) ₃ Cl] ⁺ (tétraédrique)
[Pt (NH ₃) ₃ Cl] ⁺ (plan carré)
[Ni (H ₂ O) ₄ Cl ₂]
[Co (C ₂ O ₄) ₂ Cl ₂] ³⁻ (notez qu'il$\ce{C2O4^2-}$ s'agit de l'ion oxalate bidenté,$\ce{−O2CCO2-}$)

ARTICLE 19.2.4

Le cis et le trans sont un type d'isomère géométrique, ce qui signifie qu'il existe une différence d'orientation dans laquelle les ligands sont attachés au métal central. En cis, deux des mêmes ligands sont adjacents l'un à l'autre et en trans, deux des mêmes ligands sont directement en face l'un de l'autre.

Les isomères optiques → ont la capacité de faire pivoter la lumière, les isomères optiques sont également chiraux. Seuls les complexes chiraux possèdent des isomères optiques

Chiral → asymétrique, la structure de son image miroir n'est pas superposable

Énantiomères : isomères optiques chiraux (le composé peut avoir plusieurs énantiomères)

Complexe tétraédrique à 4 ligands distincts → toujours chiral

Pour les tétraédriques, si 2 ligands sont identiques, alors il ne peut pas être chiral, possède un plan de symétrie

Des solutions :

a.$[Pt(H_2O)_2Br_2]$ (plan carré)

Ce complexe possède 2 types de ligands. Les ligands correspondants peuvent soit être adjacents les uns aux autres et être cis, soit être situés en face l'un de l'autre et être trans.

b.$[Pt(NH_3)(py)(Cl)(Br)]$ (plan carré, py = pyridine,$C_5H_5N$)

Ce complexe possède 4 ligands différents. Aucun des énantiomères n'a de plan de symétrie, ce qui rend les structures chirales et contiennent donc des isomères optiques.

c.$[Zn(NH_3)_3Cl]^+$ (tétraédrique)

Il existe un plan de symétrie de part$NH_3$$Zn$ en part$NH_3$, donc il n'est pas chiral.

d.$[Pt(NH_3)_3Cl]^+$ (plan carré)

Il existe un plan de symétrie de part$NH_3$$Pt$ en part$NH_3$, donc il n'est pas chiral.

e.$[Ni(H_2O)_2Cl_2]$

Les$Cl$ ligands peuvent être soit juste à côté l'un de l'autre, soit directement en face l'un de l'autre, ce qui permet des géométries cis et trans.

f.$[Co(C_2O_4)_2Cl_2]^-3$ (notez qu'il$C_2O_4^-2$ s'agit de l'ion oxalate bidenté,$^−O_2CCO_2^-$

Il existe un plan de symétrie allant de$Cl$ Co à l'autre$Cl$ dans une configuration de chlore « trans », donc il n'est pas chiral dans une configuration de chlore « trans ». Cependant, il n'y a aucune symétrie dans la configuration « cis » du chlore, ce qui indique de multiples isomères « cis ».

A19.2.4

a. [Pt (H ₂ O) ₂ Br ₂] :

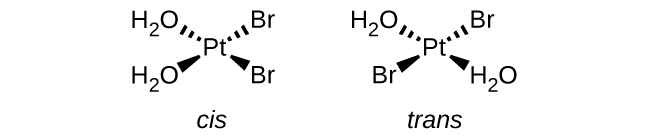
b. [Pt (NH ₃) (py) (Cl) (Br)] :

c. [Zn (NH ₃) ₃ Cl] ⁺ :

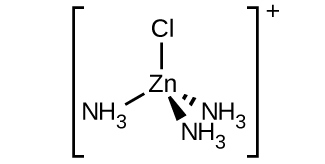
d. [Pt (NH ₃) ₃ Cl] ⁺ :

e. [Ni (H ₂ O) ₄ Cl ₂] :

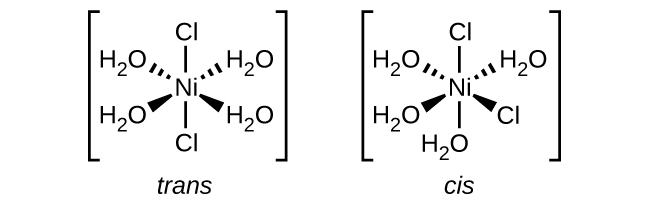
f. [Co (C ₂ O ₄) ₂ Cl ₂] ³⁻ :

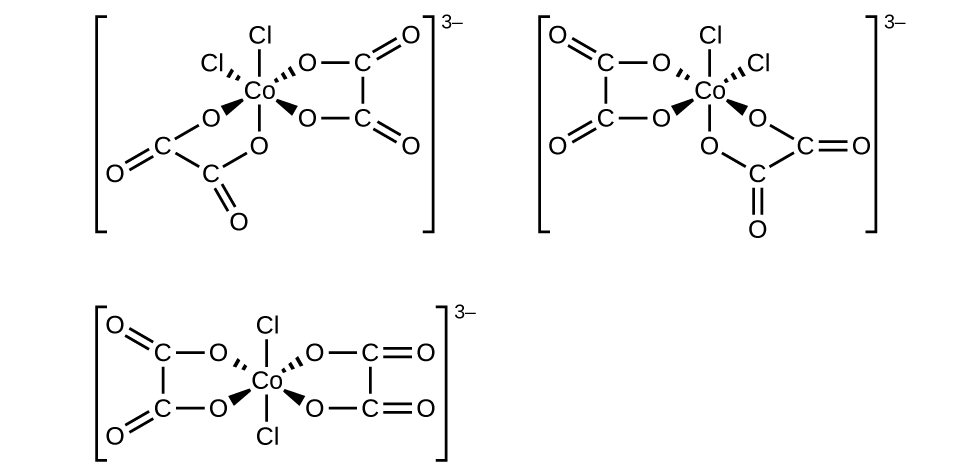
Q19.2.5

Dessinez des diagrammes pour tous les isomères cis, trans et optiques qui pourraient exister pour les composés suivants (en fait, éthylènediamine) :

[Co (fr) ₂ (NO ₂) Cl] ⁺
[Co (fr) ₂ Cl ₂] ⁺
[Pt (NH ₃) ₂ Cl ₄]
[Cr (fr) ₃] ³⁺
[Pt (NH ₃) ₂ Cl ₂]

ARTICLE 19.2.5

Nous sommes chargés de dessiner tous les isomères géométriques et les isomères optiques du composé spécifié. Les isomères optiques existent lorsqu'une configuration d'isomère n'est pas superposable à son image miroir. Cela signifie qu'il existe deux formes moléculaires distinctes. La main gauche et la main droite sont souvent citées à titre d'exemple ; si vous prenez votre main droite et que vous la placez sur votre gauche, vous ne pouvez pas aligner les parties principales de votre main l'une sur l'autre. L'idée de base pour décider si quelque chose est optiquement actif est de rechercher un plan de symétrie : si vous êtes capable de diviser un composé en deux de manière à établir la symétrie, alors le composé ne possède pas d'isomère optique.

Les isomères cis existent lorsque deux ligands de la même espèce sont placés à des angles de 90 degrés l'un de l'autre. Les isomères trans existent lorsque deux ligands de la même espèce sont placés à des angles de 180 degrés l'un de l'autre.

Problème 1

Ce composé est une molécule octaédrique, de sorte que les six ligands (atomes du complexe qui ne sont pas le métal de transition central) sont placés autour de l'atome central à des angles de 90 degrés. Deux isomères optiques existent pour le [Co (en) ₂ (NO ₂) Cl] ⁺. Le second isomère est dessiné en prenant l'image miroir du premier.

Problème 2

Ce composé est également une molécule octaédrique. Deux isomères cis (optiques) et un isomère trans existent pour le [Co (en) ₂ Cl ₂] ⁺. L'isomère trans peut être dessiné en plaçant les ligands du chlore dans des positions où ils forment un angle de 180 degrés avec l'atome central. Le premier isomère cis peut être dessiné en plaçant les ligands chlorés dans des positions où ils forment un angle de 90 degrés avec l'atome central. Le deuxième isomère cis peut être trouvé en reflétant le premier isomère cis, comme nous l'avons fait dans le problème 1.

Problème 3

Ce composé est également une molécule octaédrique. Il existe un isomère trans et un isomère cis du [Pt (NH ₃) ₂ Cl ₄]. L'isomère trans peut être dessiné en plaçant les ligands ammoniacaux dans des positions où ils forment un angle de 180 degrés avec l'atome central. L'isomère cis peut être dessiné en plaçant les ligands ammoniacaux dans des positions où ils forment un angle de 90 degrés avec l'atome central.

Problème 4

Ce composé est également une molécule octaédrique. Il existe deux isomères optiques pour le [Cr (en) ₃] ³⁺. Le second isomère optique peut être dessiné en prenant l'image miroir du premier isomère optique.

Problème 5

Ce composé est un complexe plan carré, de sorte que les ligands sont placés autour de l'atome central dans un plan, à 90 angles. Un isomère trans et un isomère cis existent pour le complexe [Pt (NH ₃) ₂ Cl ₂]. L'isomère trans peut être dessiné en plaçant les ligands ammoniacaux dans des positions où ils forment un angle de 180 degrés dans le plan avec l'atome central. L'isomère cis peut être dessiné en plaçant les ligands ammoniacaux dans des positions où ils forment un angle de 90 degrés dans le plan avec l'atome central.

Q19.2.6

Nommez chacun des composés ou ions présentés dans l'exercice Q19.2.3, en indiquant notamment l'état d'oxydation du métal.

ARTICLE 19.2.6

Règles à suivre pour les complexes de coordination

1. Les cations sont toujours nommés avant les anions.

2. Les ligands sont nommés avant l'atome métallique ou l'ion.

3. Les noms des ligands sont modifiés par l'ajout d'un ‐o au nom de racine d'un anion. Pour les ligands neutres, le nom de la molécule est utilisé, à l'exception de OH2, NH3, CO et NO.

4. Les préfixes mono‐, di‐, tri‐, tetra‐, penta‐ et hexa‐ sont utilisés pour indiquer le nombre de ligands simples.

5. Les préfixes bis‐, tris‐, tetrakis‐, etc. sont utilisés pour des ligands plus complexes ou contenant déjà du di‐, du tri‐, etc.

6. L'état d'oxydation de l'ion métallique central est désigné par un chiffre romain entre parenthèses.

7. Lorsque plus d'un type de ligand est présent, ils sont nommés par ordre alphabétique. Les préfixes n'affectent pas la commande.

8. Si l'ion complexe a une charge négative, le suffixe —ate est ajouté au nom du métal.

9. Dans le cas de l'isomérie des ions de complexe, les noms cis, trans, fac ou mer peuvent précéder la formule du nom de l'ion complexe pour indiquer la disposition spatiale des ligands. Cis signifie que les ligands occupent des positions de coordination adjacentes, et trans signifie des positions opposées, tout comme ils le font pour les composés organiques. La complexité des complexes octaédriques permet la présence de deux isomères géométriques supplémentaires qui sont propres aux complexes de coordination. Fac signifie facial, ou que les trois ligands similaires occupent les sommets d'une face de l'octaèdre. Mer signifie méridien, c'est-à-dire que les trois ligands similaires occupent les sommets d'un triangle dont un côté comprend l'atome métallique ou l'ion central.

A19.2.6

ion tricarbonatocobaltate (III) ;
ion tétraaminecoprène (II) ;
sulfate de tétraamine dibromocobalt (III) ;
tétrachloroplatinate de tétraamine platine (II) ;
nitrate de tris- (éthylènediamine) chrome (III) ;
diaminedibromopalladium (II) ;
pentachlorocuprate de potassium (II) ;
diaminedichlorozinc (II)

Q19.2.7

Nommez chacun des composés ou ions donnés dans l'exercice Q19.2.5.

ARTICLE 19.2.7

Étant donné :

[Co (fr) ₂ (NO ₂) Cl] ⁺
[Co (fr) ₂ Cl ₂] ⁺
[Pt (NH ₃) ₂ Cl ₄]
[Cr (fr) ₃] ³⁺
[Pt (NH ₃) ₂ Cl ₂]

Souhaité :

Noms des composés ci-dessus.

1. [Co (fr) ₂ (NO ₂) Cl] ⁺

Étape 1 : Obtenir les noms des ligands et des cations métalliques. Les noms peuvent être trouvés ici.

Co : Cobalt

fr : Ethylenediamine

N° ₂ : Nitro

Cl : Chloro

Étape 2 : Ajoutez les préfixes appropriés à chaque ligand en fonction du nombre. Les préfixes peuvent être trouvés ici.

(fr) ₂ : bis (éthylènediamine)

Étape 3 : Trouvez les charges des ligands. Les frais peuvent être consultés ici.

fr : 0

N° ₂ : -1

Cl : -1

Étape 4 : Atteindre algébriquement la charge du cation métallique en utilisant la charge globale de l'ion complexe et les charges individuelles du ligand.

Co + 2 (fr) + (NO ₂) + Cl = 1

Co +2 (0) + (-1) + (-1) = 1

Co = 3

Étape 5 : Pour le nom, placez les ligands par ordre alphabétique, sans prendre en compte les préfixes, et utilisez des chiffres romains pour le cation métallique qui doit être placé en dernier.

Chlorobis (éthylènediamine) nitrocobalt (III)

2. [Co (fr) ₂ Cl ₂] ⁺

Étape 1 : Obtenir les noms des ligands et des cations métalliques. Les noms peuvent être trouvés ici.

Co : Cobalt

fr : Ethylenediamine

Cl : Chloro

Étape 2 : Ajoutez les préfixes appropriés à chaque ligand en fonction du nombre. Les préfixes peuvent être trouvés ici.

(fr) ₂ : bis (éthylènediamine)

Cl ₂ : dichloro

Étape 3 : Trouvez les charges des ligands. Les frais peuvent être consultés ici.

fr : 0

Cl : -1

Étape 4 : Atteindre algébriquement la charge du cation métallique en utilisant la charge globale de l'ion complexe et les charges individuelles du ligand.

Co + 2 (fr) +2 (Cl) = 1

Co + 2 (0) + 2 (-1) = 1

Co = 3

Dichlorobis (éthylènediamine) cobalt (III)

3. [Pt (NH ₃) ₂ Cl ₄]

Étape 1 : Obtenir les noms des ligands et des cations métalliques. Les noms peuvent être trouvés ici.

Pt : Platine

NH ₃ : Ammine

Cl : Chloro

Étape 2 : Ajoutez les préfixes appropriés à chaque ligand en fonction du nombre. Les préfixes peuvent être trouvés ici.

(NH _₃₂) : diamant

Cl ₄ : tétrachloro

Étape 3 : Trouvez les charges des ligands. Les frais peuvent être consultés ici.

NH ₃ : 0

Cl : -1

Étape 4 : Atteindre algébriquement la charge du cation métallique en utilisant la charge globale de l'ion complexe et les charges individuelles du ligand.

Pt + 2 (NH ₃) + 4 (Cl) = 0

Pt + 2 (0) + 4 (-1) = 0

Animaux de compagnie = 4

Diamminettétrachloroplatine (IV)

4. [Cr (fr) ₃] ³⁺

Étape 1 : Obtenir les noms des ligands et des cations métalliques. Les noms peuvent être trouvés ici.

Voiture : Chromium

fr : éthylènediamine

Étape 2 : Ajoutez les préfixes appropriés à chaque ligand en fonction du nombre. Les préfixes peuvent être trouvés ici.

(fr) ₃ : tris (éthylènediamine)

Étape 3 : Trouvez les charges des ligands. Les frais peuvent être consultés ici.

fr : 0

Étape 4 : Atteindre algébriquement la charge du cation métallique en utilisant la charge globale de l'ion complexe et les charges individuelles du ligand.

Cr + 3 (fr) = 3

Cr + 3 (0) = 3

Cr = 3

Tris (éthylènediamine) chrome (III)

5. [Pt (NH ₃) ₂ Cl ₂]

Étape 1 : Obtenir les noms des ligands et des cations métalliques. Les noms peuvent être trouvés ici.

NH ₃ : Ammine

Cl : Chloro

Pt : Platine

Étape 2 : Ajoutez les préfixes appropriés à chaque ligand en fonction du nombre.

(NH _₃₂) : diamant

Cl ₂ : dichloro

Étape 3 : Trouvez les charges des ligands. Les frais peuvent être consultés ici.

NH ₃ : 0

Cl : -1

Étape 4 : Atteindre algébriquement la charge du cation métallique en utilisant la charge globale de l'ion complexe et les charges individuelles du ligand.

Pt + 2 (NH ₃) +2 (Cl) = 0

Pt + 2 (0) + 2 (-1) = 0

Animaux de compagnie = 2

Dichloroplatine diamminé (II)

A19.2.7

Chlorobis (éthylènediamine) nitrocobalt (III)
Dichlorobis (éthylènediamine) cobalt (III)
Diamminettétrachloroplatine (IV)
Tris (éthylènediamine) chrome (III)
Diamminedichloroplatine (II)

Q19.2.8

Précisez si les complexes suivants contiennent des isomères.

tétraédrique [Ni (CO) ₂ (Cl) ₂]
bipyramidal trigonal [Mn (CO) ₄ NO]
[Pt (fr) ₂ Cl ₂] Cl ₂

ARTICLE 19.2.8

Les isomères sont des composés qui ont le même nombre d'atomes, mais qui ont des structures différentes. Des isomères structuraux (liaison, ionisation, coordination) et des stéréoisomères (géométriques et optiques) peuvent apparaître avec plusieurs composés.

1. tétraédrique$\mathrm{[Ni(CO)_2(Cl)_2]}$

(Figure 1.) Dans ce modèle, le nickel est l'atome central vert foncé, les ligands carbonyle l'atome rose et les ligands chlorés les atomes vert clair.

Nous pouvons immédiatement annuler la possibilité d'isomères de liaison, d'ionisation et de coordination. Il n'existe aucun autre complexe de coordination pour l'isomérie de coordination, aucun ligand ne peut se lier à l'atome de plus d'une façon pour que celui-ci présente un isomérie de liaison, et aucun ion ne se trouve en dehors de la sphère de coordination pour l'isomérie d'ionisation.

Il s'agit d'une structure tétraédrique qui exclut immédiatement tout isomère géométrique puisqu'ils nécessitent des angles de liaison de 90° et/ou 180°. Les structures tétraédriques présentent des angles de 109,5°.

Pour confirmer que la structure ne possède pas d'isomère optique, il faut déterminer s'il existe un plan de symétrie. Les structures qui n'ont pas de plan de symétrie sont considérées comme chirales et comporteraient des isomères optiques.

(Figure 2.) Nous pouvons faire pivoter la structure et constater qu'il existe bien un plan de symétrie entre les deux ligands chlorés et l'atome central et entre les ligands carbonylés.

Comme il existe un plan de symétrie, nous pouvons conclure qu'il n'y a pas d'isomères optiques.

Dans l'ensemble, il n'existe aucun isomère pour ce composé.

2. trigonal par primidal$\mathrm{[Mn(CO)_4(NO)]}$

(Figure 3.) L'atome violet central est le manganèse, les ligands carbonylés sont les atomes roses et le ligand nitrosyle est l'atome de fuschia.

Il n'y a pas d'ions, d'autres complexes de coordination et de ligands ambidentés. Il n'existe donc aucun isomère structural pour cette structure.

Il n'existe pas d'isomères géométriques pour ce composé car il n'existe qu'un seul ligand nitrosyle.

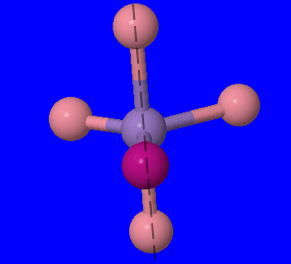
(Figure 4.) La ligne pointillée divise la molécule en deux et indique le plan de symétrie. La molécule est mise en rotation sur cette image.

Dans l'image ci-dessus, après la rotation de la structure, nous pouvons voir qu'il existe un plan de symétrie. Il n'y a donc pas d'isomères optiques.

Il n'existe aucun isomère (ceux mentionnés ci-dessus) pour ce composé.

3. $\mathrm{[Pt(en)_{2}Cl_2]Cl_2}$

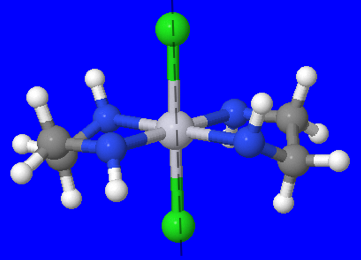
(Figure 5.) Les atomes verts sont les ligands chlorés, l'atome central est le platine et les atomes gris/bleu sont des ligands d'éthyldiamine.

L'isomérie de coordination ne peut pas exister pour ce complexe car il n'existe aucun autre complexe. Il n'y a pas d'isomères de liaison car il n'y a pas de ligands ambidentés. Les isomères d'ionisation ne peuvent pas non plus exister dans ce complexe, même s'il existe une molécule neutre en dehors de la sphère de coordination. Si nous échangeons$\mathrm{Cl_2}$ avec une molécule d'éthyldiamine, il y aurait 5 ligands dans la sphère de coordination au lieu de 4. Cette différence dans le rapport entre l'atome métallique et les ligands signifie qu'un isomère d'ionisation ne peut pas exister.

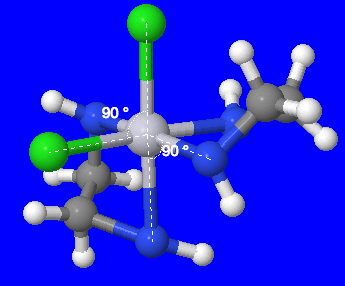
(Figure 6.) Ici, un ligand chloré a échangé sa place avec l'éthyldiamine de sorte qu'il puisse former un angle de 90° avec l'autre ligand chloré.

L'image ci-dessus montre les ligands chloro et éthyldiamine à un angle de 90° avec son autre ligand identique. Il s'agit de l'isomère cis, tandis que la figure 5 montre l'isomère trans.

La figure 5 montre qu'il existe un plan de symétrie dans l'isomère trans. Cette structure ne possède donc pas d'isomère optique. En revanche, l'isomère cis ne possède pas de plan de symétrie et possède donc un isomère optique.

A19.2.8

aucun ; aucun ; Les deux ligands Cl peuvent être cis ou trans. Lorsqu'ils sont cis, il y aura également un isomère optique.

Q19.2.9

Prédisez si le ligand carbonate$\ce{CO3^2-}$ se coordonnera avec un centre métallique sous la forme d'un ligand monodenté, bidenté ou tridenté.

S19.2.9

$\ce{CO3^2−}$peut être monodenté ou bidenté, puisque deux de ses atomes d'oxygène ont des paires isolées, comme indiqué ci-dessus, et peuvent former des liaisons covalentes avec un ion de métal de transition. Dans la plupart des cas, le carbonate est monodenté en raison de sa géométrie plane trigonale (il y a 120 degrés entre les oxygènes, il est donc difficile pour les deux de se lier au même métal). Cependant, dans certains cas, il se lie à deux métaux différents, le rendant bidenté.

A19.2.9

Le CO ₃ ^-2 se coordonnera avec un centre métallique sous la forme d'un ligand monodenté.

Q19.2.10

Dessinez les isomères géométriques, de liaison et d'ionisation pour [CoCl ₅ CN] [CN].

S19.2.10

Les isomères sont des composés ayant la même formule mais une disposition atomique différente. Il existe deux sous-catégories : les isomères structuraux, qui sont des isomères contenant le même nombre d'atomes de chaque type mais dont les atomes sont liés les uns aux autres, et les stéréoisomères, des isomères qui ont la même formule moléculaire et les mêmes ligands, mais dont la disposition diffère. des ligands dans un espace 3D.

Il existe trois sous-catégories sous les isomères structuraux : les isomères d'ionisation, qui sont des isomères identiques à l'exception d'un ligand qui a des points d'échange avec un anion ou une molécule neutre qui se trouvait à l'origine en dehors du complexe de coordination ; les isomères de coordination, les isomères qui ont un échange de certains ligands de la partie cationique à la partie anionique ; et des isomères de liaison, dans au moins deux composés de coordination dans lesquels l'atome donneur d'au moins un des ligands est différent.

Il existe également deux types principaux de stéréoisomères : les isomères géométriques, les complexes métalliques qui ne diffèrent que par le fait que les ligands sont adjacents les uns aux autres (cis) ou directement en face l'un de l'autre (trans) dans la sphère de coordination du métal, et les isomères optiques, qui se produisent lorsque le miroir l'image d'un objet n'est pas superposable à l'objet d'origine.

Certains isomères semblent presque identiques, mais c'est parce que le ligand CN peut être attaché à la fois par le C ou le N.

A19.2.10

19.3 : Propriétés spectroscopiques et magnétiques des composés de coordination

Q19.3.1

Déterminer le nombre d'électrons non appariés attendus pour le [Fe (NO ₂) ₆] ³⁻ et pour le [FeF ₆] ³⁻ en termes de théorie des champs cristallins.

ARTICLE 19.3.1

La théorie des champs cristallins est un modèle qui décrit la rupture des dégénérescences des états orbitaux des électrons, généralement des orbitales d ou f, en raison d'un champ électrique statique produit par une distribution de charge environnante.
Les orbitales d dégénérées se divisent en deux niveaux, e$_{g}$ et t$_{2g}$, en présence de ligands.
La différence d'énergie entre les deux niveaux est appelée énergie de division du champ cristallin,$\Delta_{\circ}$.
Une fois qu'un électron a été rempli dans les trois$_{2g}$ orbitales t, le remplissage du quatrième électron a lieu soit dans l'$_{g}$orbitale e, soit dans l'orbitale t$_{2g}$, où les électrons s'apparient, selon que le complexe est à spin élevé ou à spin faible.
Si la$\Delta_{\circ}$ valeur d'un ligand est inférieure à l'énergie d'appariement (P), les électrons entrent sur l'$_{g}$orbitale e, mais si la$\Delta_{\circ}$ valeur d'un ligand est supérieure à l'énergie d'appariement (P), alors les électrons entrent sur l'$_{2g}$orbitale t.
lorsque la valeur $\Delta_o$ est inférieure à l'énergie d'appariement, les électrons préfèrent les orbitales, _par exemple parce qu'il n'y a pas assez d'énergie pour jumeler les électrons entre eux. Ce sera un spin élevé
lorsque la valeur $\Delta_o$ est supérieure à l'énergie d'appariement, les électrons préfèrent la t _2g car il y a suffisamment d'énergie pour jumeler les électrons. Ce sera un spin faible.

Étape 1 : Déterminer l'état d'oxydation du Fe

Pour$[Fe(NO_{2}){_{6}}]^{3-}$ et$[FeF_{6}]^{3-}$, les deux$NO_{2}$ et$F_{6}$ ont une charge de -1. Comme il y en a 6, cela signifie que la charge est de -6 et pour qu'il y ait une charge globale de -3, le Fe doit avoir une charge de +3.

Étape 2 : Déterminer le type de ligand

Sur la base de la série spectrochimique$^{-}$, nous pouvons voir qu'il$NO_{2}^{-}$ s'agit d'un ligand de champ plus fort que F et qu'il s'agit donc d'un complexe à faible spin car il a un fort$\Delta_{\circ}$ contrairement à F$^{-}$ qui est un spin élevé.

Étape 3 : Dessinez le champ de cristal

$[Fe(NO_{2}){_{6}}]^{3-}$

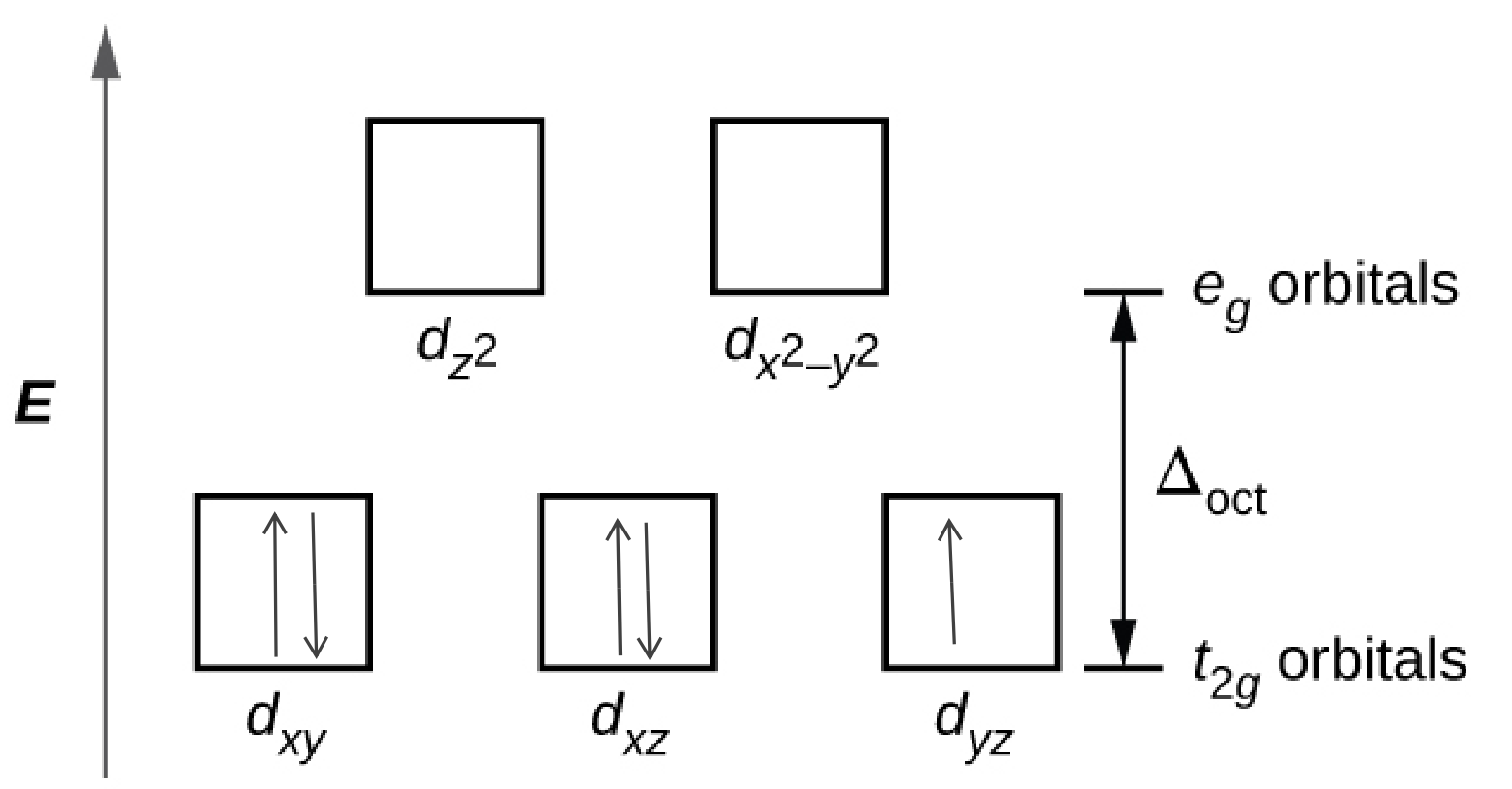
$[FeF_{6}]^{3-}$

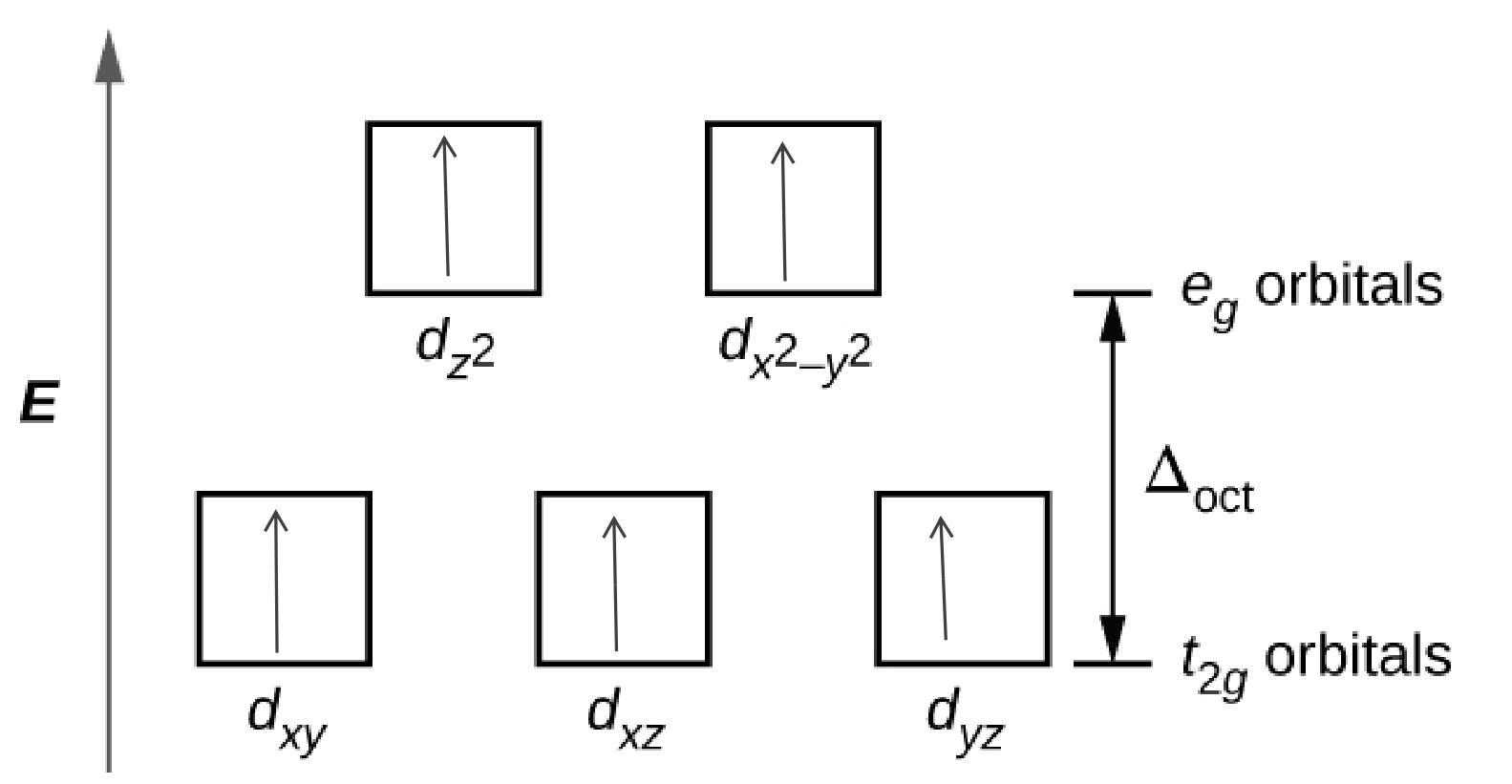
Il y a 1 électron non apparié pour$[Fe(NO_{2}){_{6}}]^{3-}$, et 5 pour,$[FeF_{6}]^{3-}$ selon la théorie des champs cristallins.

A19.3.1

[Fe (NO ₂) ₆] Électron ^3−:1

[FeF ₆] ^3−:5 électrons

Q19.3.2

Dessinez les diagrammes des champs cristallins pour le [Fe (NO ₂) ₆] ⁴⁻ et le [FeF ₆] ²⁻. Indiquez si chaque complexe est à spin élevé ou à spin faible, paramagnétique ou diamagnétique, et comparez Δ _oct à P pour chaque complexe.

ARTICLE 19.3.2

a)\[[Fe(NO_2)_6]^{_{-4}}\]

NO ₂ ^- a une charge de -1. L'ion global a une charge de -4, donc le Fe doit avoir une charge de +2. (Le calcul : $x+(6)(-1)=-4, x+-6=-4, x=+2$ou 2+ (6*-1) =-4)
Le Fe ²⁺ possède 6 électrons de valence.
Ensuite, nous examinons le ligand lié au Fe, qui est le NO ₂ ^-. ^{Sur la base de la série spectrochimique, le NO ₂ est un ligand à champ puissant, ce qui signifie qu'il possède une grande énergie de division DELTA _o grande par rapport à l'énergie d'appariement, P. Les électrons préfèrent donc s'apparier, car cela demande le moins d'énergie.}
Donc, [Fe (NO ₂) ₆] ⁴⁻ a un faible spin.
Les 6 électrons sont jumelés, donc ils sont diamagnétiques.

b)\[[FeF_6]^{_{-3}}\]

F ^- a une charge de -1. L'ion global a une charge de -3, donc le Fe doit avoir une charge de +3. (Le calcul : $x+(-1)(6)=-3, x+-6=-3, x=+3$ou 3+ (6*-1) =-3)
F ^³⁺ possède 5 électrons de valence.
Ensuite, nous examinons le ligand lié au Fe, qui est F ^-. Sur la base de la série spectrochimique, F ^- est un ligand de champ faible, ce qui signifie qu'il possède un petit DELTA _o ou une faible énergie de division par rapport à l'énergie d'appariement, P. Les électrons préfèrent donc se séparer et monter au niveau d'énergie le plus élevé, plutôt que de s'apparier, car il faut le moins d'énergie possible.
Donc, [Fe (NO ₂) ₆] ⁴⁻ a un spin élevé.
Le [FeF ₆] ³⁻ est paramagnétique car il contient des électrons non appariés.

A19.3.2

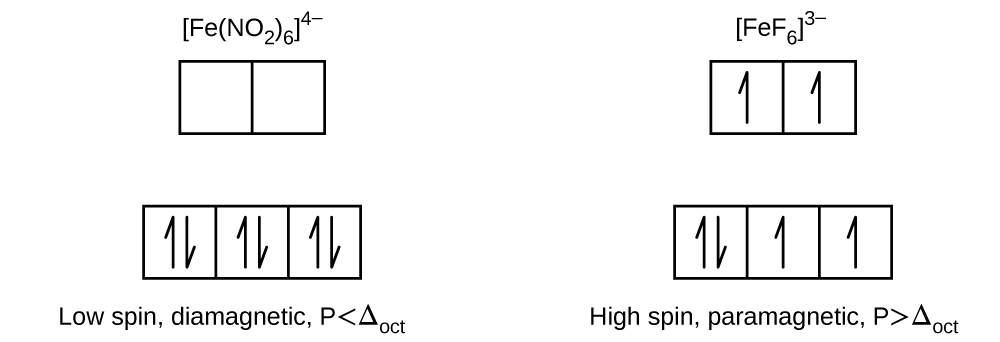
Q19.3.3

Donnez l'état d'oxydation du métal, le nombre d'électrons d et le nombre d'électrons non appariés prévus pour le [Co (NH ₃) ₆] Cl ₃.

ARTICLE 19.3.3

L'état d'oxydation du métal peut être déterminé en identifiant la charge d'une molécule de chaque molécule dans le composé coordonné, en multipliant la charge de chaque molécule par le nombre respectif de molécules présentes et en ajoutant les produits. Cette somme finale représente la charge du complexe de coordination global. Vous pouvez ensuite déterminer l'état d'oxydation du métal de manière algébrique. Dans ce cas, un anion chlorure Cl ^- a une charge de -1. Trois anions chlorure ont donc une charge totale de -3. Un ligand amine NH ₃ n'a aucune charge, donc six ligands amines ont une charge totale nulle. Enfin, nous essayons de déterminer l'état d'oxydation d'un ion cobalt. Nous pouvons maintenant écrire l'équation qui additionne les charges totales de chaque molécule ou ion et qui est égale à la charge totale du composé coordonné global.

\[ (\text{oxidation}\text{ state}\text{ of}\text{ Co})+(-3)+0=0 \]

\[ \text{oxidation}\text{ state}\text{ of}\text{ Co}=+3 \]

L'état d'oxydation du Co est donc de +3. Nous devons maintenant identifier le nombre d'électrons d dans l'ion Co ³⁺. La configuration électronique du cobalt sans charge est

\[ [\text{Ar}]4\text{s}^23\text{d}^7 \]

Cependant, un ion Co ³⁺ possède 3 électrons de moins que son homologue neutre et a une configuration électronique de

\[ [\text{Ar}]3\text{d}^6 \]

Pour les métaux de transition, les$ \text{s} $ électrons sont perdus en premier. Le cobalt perd donc d'abord ses deux$ 4\text{s} $ électrons, puis perd un seul$ 3\text{d} $ électron, ce qui signifie que l'ion Co ³⁺ possède 6$ \text{d} $ électrons. Pour prédire le nombre d'électrons non appariés, nous devons d'abord déterminer si le complexe est à spin élevé ou à spin faible. Le fait que le complexe soit à spin élevé ou à spin faible est déterminé par le ligand du complexe de coordonnées. Plus précisément, le ligand doit être identifié comme un ligand à champ faible ou un ligand à champ fort sur la base de la série spectrochimique. Les ligands à champ faible induisent un spin élevé tandis que les ligands à champ fort induisent un spin faible. Nous pouvons ensuite construire le diagramme d'énergie ou le diagramme du champ cristallin du spin désigné qui possède les emplacements électroniques appropriés. La forme géométrique du composé doit également être identifiée pour construire le diagramme correct. Enfin, à partir de ce diagramme de champ cristallin, nous pouvons déterminer le nombre d'électrons non appariés. Le nombre d'électrons sur le diagramme est égal au nombre d'$ \text{d} $électrons du métal. Le ligand dans ce cas est le NH ₃, qui est un ligand de champ fort selon la série spectrochimique. Cela signifie que le complexe a un faible spin. De plus, six ligands monodentés signifient que le champ de ligands est octaédrique. Le nombre d'électrons qui figureront sur le diagramme est de 6 puisque l'ion métallique Co ³⁺ possède 6$ \text{d} $ électrons. Le diagramme de champ cristallin approprié peut maintenant être construit.

À partir du diagramme du champ cristallin, nous pouvons dire que le complexe ne possède pas d'électrons non appariés.

A19.3.3

a) Plus de 3

b) 6 électrons d

c) Aucun électron non apparié

Q19.3.4

Le solide anhydre CoCl ₂ est de couleur bleue. Comme il absorbe facilement l'eau de l'air, il est utilisé comme indicateur d'humidité pour vérifier si un équipement (tel qu'un téléphone portable) a été exposé à des niveaux d'humidité excessifs. Prédisez quel produit est formé par cette réaction et combien d'électrons non appariés contiendra ce complexe.

S19.3.4

Sur la base de nos connaissances sur les ligands et les composés de coordination (ou si vous avez besoin d'un complément d'information sur les composés de coordination), nous pouvons supposer le produit du CoCl ₂ dans l'eau. Le H ₂ O est un ligand à champ faible courant qui forme six liaisons ligands autour de l'atome de cobalt central tandis que le chlorure reste sur la sphère extérieure. Nous pouvons l'utiliser pour déterminer le complexe :

$[Co(H_2O)_6]Cl_2$

À partir de cette formation, nous pouvons utiliser la théorie des champs cristallins (CFT) (théorie des champs cristallins) pour déterminer le nombre d'électrons non appariés. Ce composé de coordination possède six liaisons ligands attachées à l'atome central, ce qui signifie que le modèle CFT suivra la division octaédrique. Gardez à l'esprit que nous savons que le H ₂ O est un ligand à faible champ qui produira un spin élevé. Un spin élevé se produit lorsque l'énergie d'appariement des électrons (P) est supérieure à l'énergie de division octaédrique. Ainsi, les électrons s'étalent et maximisent le spin.

Afin de remplir notre diagramme de champ cristallin, nous devons déterminer la charge du cobalt. Comme le ligand H ₂ O est neutre et qu'il y a deux ions chlore, nous pouvons déduire que la charge de cobalt est plus deux afin de rendre le complexe de coordination neutre. À partir de là, nous pouvons utiliser la configuration électronique du Co ^{2+ est} [Ar] 4s ² 3d ⁷. Les électrons qui sont retirés de l'atome de cobalt pour former la charge plus deux sortiront de l'orbitale 4s et laisseront la 3e orbitale intacte. Ainsi, il y aura 7 électrons dans le diagramme du champ cristallin et apparaîtront comme suit :

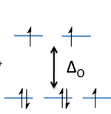
On peut voir ici qu'il y a 3 électrons non appariés.

A19.3.4

[Co (H ₂ O) ₆] Cl ₂ avec trois électrons non appariés.

Q19.3.5

Est-il possible qu'un complexe d'un métal de la série de transition possède six électrons non appariés ? Expliquez.

A19.3.5

Est-il possible qu'un complexe d'un métal de la série de transition possède six électrons non appariés ? Expliquez.

Il n'est pas possible qu'un métal de la série de transition possède six électrons non appariés. Cela est dû au fait que les métaux de transition ont une configuration électronique générale de (n-1) d ^1-10 ns ^1-2 où n est le nombre quantique. Le dernier électron ira sur l'orbitale d qui possède 5 orbitales pouvant contenir chacune 2 électrons, soit 10 électrons au total. Selon la règle de Hund, les électrons préfèrent remplir chaque orbitale individuellement avant de s'apparier. C'est plus favorable sur le plan énergétique. Comme il n'y a que 5 orbitales et en raison de la règle de Hund, le nombre maximum d'électrons non appariés qu'un métal de transition peut avoir est de 5. Il ne peut donc pas y avoir de complexe de métal de transition contenant 6 électrons non appariés.

Par exemple, examinons la configuration électronique du fer. Le fer a une configuration électronique de 1s ² 2s ² 2p ⁶ 3s ² 3p ⁶ 4s ² 3d ⁶. Maintenant, l'orbitale la plus importante à examiner est l'orbitale d qui contient 6 électrons, mais il n'y a que 4 électrons non appariés, comme vous pouvez le voir sur ce schéma :

3d : [] [] [] [] []

Chaque [] représente une orbitale au sein de l'orbitale d. Ce diagramme suit la règle de Hund et montre pourquoi aucun métal de transition ne peut avoir 6 électrons non appariés.

Q19.3.6

Combien d'électrons non appariés sont présents dans chacun des éléments suivants ?

[CoF ₆] ³⁻ (spin élevé)
[Mn (CN) ₆] ³⁻ (rotation lente)
[Mn (CN) ₆] ⁴⁻ (rotation lente)
[MnCl ₆] ⁴⁻ (spin élevé)
[RhCl ₆] ³⁻ (faible spin)

ARTICLE 19.3.6

1. Pour le [CoF ₆] ^3-, nous avons d'abord trouvé l'état d'oxydation du Co, qui est de 3+ puisque F a une charge 1- et comme il y a 6 F, la charge de Co doit être de 3+ pour que la charge globale soit de 3-.

\[\textrm{charge of Co} + \textrm{-6} = \textrm{-6}\]\[\textrm{charge of Co} = \textrm{+3}\]

Après avoir trouvé l'état d'oxydation, je passe ensuite au tableau périodique pour trouver sa configuration électronique : [Ar] 3d ⁶

Nous distribuons les 6 électrons de l'orbite D le long du complexe et, comme le spin est élevé, les électrons sont distribués une fois par niveau d'énergie avant d'être appariés. Il n'y a qu'une seule paire et les 4 autres électrons ne sont pas appariés, ce qui fait que la réponse est 4.

2. Le même processus est répété. Nous trouvons la charge de Mn, qui est de 3+, donnant la configuration électronique : [Ar] 3d ⁴

\[\textrm{charge of Mn} + \textrm{-6} = \textrm{-3}\]\[\textrm{charge of Mn} = \textrm{+3}\]

Il y a une différence entre ce chiffre et le numéro 1. Le spin est faible donc au lieu de distribuer un électron dans chaque niveau avant de l'apparier, je dois distribuer un électron en bas, puis les jumeler tous avant de pouvoir passer à la partie supérieure. Donc, comme il y a 4, il n'y a qu'une paire à d _yz et les deux autres électrons ne sont pas appariés. Déterminer le nombre d'électrons non appariés 2.

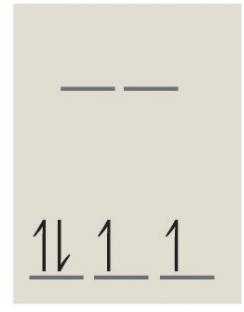
3. Le même processus que le numéro 2 est appliqué. La seule différence est que la charge de Mn est maintenant de 2+, donc la configuration électronique : [Ar] 3d ⁵.

\[\textrm{charge of Mn} + \textrm{-6} = \textrm{-4}\]\[\textrm{charge of Mn} = \textrm{+2}\]

Comme il s'agit d'un spin faible comme le numéro 2, il me suffit d'ajouter un électron supplémentaire au niveau suivant, ce qui fait que 2 paires d'électrons et un seul électron ne sont pas appariés.

4. Puisque Cl a une charge -1 comme CN, la charge de Mn est également de 2+ avec la même configuration électronique que le numéro 3, qui est 5.

\[\textrm{charge of Mn} + \textrm{-6} = \textrm{-4}\]\[\textrm{charge of Mn} = \textrm{+2}\]

Avec 5 électrons, c'est un spin élevé au lieu de faible. Ainsi, comme indiqué dans le numéro 1, nous distribuons d'abord les électrons à tous les niveaux. Comme il y a 5 électrons et 5 niveaux et qu'ils sont tous distribués, il n'y a aucune paire, ce qui fait 5 électrons non appariés.

5. En utilisant le même processus que pour les problèmes ci-dessus, la charge de Rh est de 3+, avec la configuration électronique : [Kr] 4d ⁶.

\[\textrm{charge of Rh} + \textrm{-6} = \textrm{-3}\]\[\textrm{charge of Mn} = \textrm{+3}\]

Avec un faible spin et 6 électrons, tous les électrons sont appariés, ce qui fait 0 électron non apparié.

A19.3.6

4 ; 2 ; 1 ; 5 ; 0

Q19.3.7

Expliquez comment l'ion diphosphate, [O ₃ P−O−PO ₃] ⁴⁻, peut fonctionner comme un adoucisseur d'eau qui empêche la précipitation du Fe ²⁺ sous forme de sel de fer insoluble.

ARTICLE 19.3.7

L'ion diphosphate, [O ₃ P−O−PO ₃] ⁴⁻ peut fonctionner comme un adoucisseur d'eau, maintenant le fer sous une forme soluble dans l'eau en raison de son potentiel électrochimique plus négatif que celui de l'eau. Cela est similaire à la façon dont le placage empêche les métaux de réagir avec l'oxygène pour se corroder.

Les dépôts minéraux sont formés par des réactions ioniques. Le Fe ²⁺ formera un sel de fer insoluble d'hydroxyde d'oxyde de fer (III) lorsqu'un sel de fer ferrique hydrolyse l'eau. Cependant, avec l'ajout de [O ₃ P−O−PO ₃] ⁴⁻, les cations Fe ²⁺ sont davantage attirés par le groupe PO ₃, formant un complexe Fe (PO ₃).

L'excès de minéraux dans ce type d'eau est considéré comme dur, d'où son nom d'eau dure.

Q19.3.8

Pour les complexes du même ion métallique dont le nombre d'oxydation ne change pas, la stabilité augmente à mesure que le nombre d'électrons dans les orbitales t _{2 g} augmente. Quel complexe de chacune des paires de complexes suivantes est le plus stable ?

[Fe (H ₂ O) ₆] ²⁺ ou [Fe (CN) ₆] ⁴⁻
[Co (NH ₃) ₆] ³⁺ ou [CoF ₆] ³⁻
[Mn (CN) ₆] ⁴⁻ ou [MnCl ₆] ⁴⁻

S19.3.8

La série spectrochimique est la suivante\[I^{-}<Br^{-}<SCN^{-}\approx Cl^{-}<F^{-}<OH^{-}<ONO^{-}<ox<H_{2}O<SCN^{-}<EDTA<NH_{3}<en<NO_{2}^{-}<CN\]

Les ligands de champ puissant (à droite) ont un spin faible qui remplit davantage d'électrons dans les orbitales t _{2 g.} Les ligands de champ faible (à gauche) ont un spin élevé, ce qui leur permet de remplir les électrons des orbitales t _{2 g} _{et e g.} En conclusion, davantage d'électrons sont remplis à partir des ligands de champ puissant parce que les électrons ne se déplacent pas jusqu'aux orbitales _, par exemple.

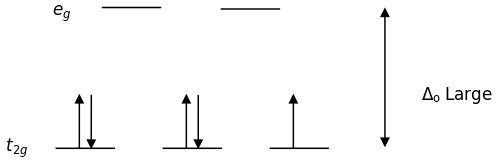
un.$[Fe(CN)_{6}]^{4-}$

$CN$est un ligand plus fort$H_{2}O$ que cela, il a un faible spin, qui remplit les orbitales t _{2 g.}

b.$[Co(NH_{3})_{6}]^{3+}$

$NH_{3}$est un ligand plus fort que$F$.

c.$[Mn(CN)_{6}]^{4-}$

$CN$est un ligand plus fort que$Cl^{-}$.

Pour plus d'informations sur la forme du complexe et la configuration des électrons D, libretext fournit plus d'informations sur la façon de classer les complexes à spin élevé et faible.

A19.3.8

[Fe (CN) ₆] ⁴⁻ ; [Co (NH ₃) ₆] ³⁺ ; [Mn (CN) ₆] ⁴⁻

Q19.3.9

La triméthylphosphine, P (CH ₃) ₃, peut agir comme un ligand en donnant la seule paire d'électrons sur l'atome de phosphore. Si de la triméthylphosphine est ajoutée à une solution de chlorure de nickel (II) dans de l'acétone, un composé bleu ayant une masse moléculaire d'environ 270 g et contenant 21,5 % de Ni, 26,0 % de Cl et 52,5 % de P (CH ₃) ₃ peut être isolé. Ce composé bleu ne présente aucune forme isomérique. Quelles sont la géométrie et la formule moléculaire du composé bleu ?

S19.3.9

1) Trouvez la formule empirique. Il y a un total de 270 grammes. Pour connaître le nombre de grammes de chaque élément/composé, multipliez le pourcentage par la masse (270).

\[(270g)(0.215)=58.05gNi\]

\[(270g)(0.26)=70.2gCl\]

\[(270g)(0.525)=141.75gP(CH_3)_3\]

Maintenant que nous avons les grammes de chaque élément/composé, nous pouvons les convertir en moles en utilisant leur masse molaire.

\[(58.055gNi)(\frac{1mol.}{58.69gNi})=0.989mol.Ni\]

\[(70.2gCl)(\frac{1mol.}{35.45gCl})=1.98mol.Cl\]

\[(141.75gP(CH_3)_3)(\frac{1mol.}{76.07gP(CH_3)_3})=1.86mol.P(CH_3)_3\]

Maintenant que nous avons les moles de tous les éléments/composés, nous pouvons trouver le rapport entre eux. Pour ce faire, nous prenons l'élément/composé contenant le moins de moles et divisons toutes les moles éléments/composés par cette quantité. Dans ce cas, Ni a le moins de moles.

\[\frac{0.989mol.Ni}{0.989mol.Ni}=1\]

\[\frac{1.98mol.Cl}{0.989mol.Ni}=approx.2\]

\[\frac{1.86mol.P(CH_3)_3}{0.989mol.Ni}=approx.2\]

Nous connaissons maintenant le ratio de tous les éléments/composés dans le composé bleu.

La formule empirique est la suivante : NiCl (P (CH ₃) ₃) ₂

Cette formule nous montre qu'il existe 4 ligands. Il existe 2 ligands du chlore et 2 ligands de la triméthylphosphine. Cela signifie que le composé bleu a une forme plane tétraédrique ou carrée, où les formes tétraédriques peuvent prendre différentes formes isomériques lorsque tous les ligands sont différents (car sinon, il n'y a qu'une seule façon de les disposer), et les formes planes carrées peuvent prendre des formes cis/trans. Dans le problème, il est indiqué que ce composé ne possède aucune forme isomérique, donc qu'il a une forme tétraédrique.

A19.3.9

a) NiCl (P (CH _₃) ₃₂)

b) Tétraédrique

Q19.3.10

Vous attendez-vous à ce que le complexe [Co (en) ₃] Cl ₃ contienne des électrons non appariés ? Des isomères ?

S19.3.10

Attribuez des états d'oxydation à chaque élément. Le Cl- a un état d'oxydation -1. En est neutre, donc 0. L'ensemble du complexe est également neutre, donc pour équilibrer les charges, Co doit être de +3 car il y a 3 chlorures, ce qui donne une charge de -3.

ÉTAPE 2 :

Ecrivez la configuration électronique pour$Co^{3+}$. $[Ar]3d^6$. Il y a 6 électrons.

ÉTAPE 3 :

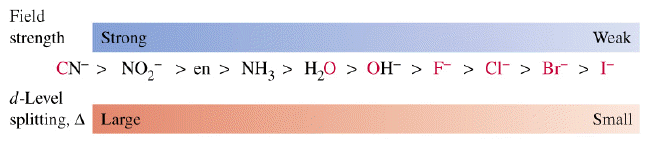
Vérifiez où se situe la fin de la série spectrochimique. Est-ce qu'il a une forte intensité de champ ? C'est le cas, de sorte que ces électrons existeront au niveau d avec une énergie de division élevée parce que l'amplitude de l'énergie d'appariement est inférieure à l'énergie de division du champ cristallin dans le champ octaédrique.

Vous remarquerez qu'il n'y a pas d'électrons non appariés lorsque vous dessinez le diagramme de la théorie des champs cristallins (CFT).

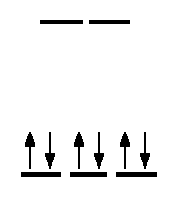
Ce complexe ne possède aucun isomère géométrique car les structures cis-trans ne peuvent pas se former. L'image miroir n'est pas superposable, ce qui signifie que les énantiomères sont des molécules chirales ; si l'image miroir est placée au-dessus de la molécule d'origine, ils ne seront jamais parfaitement alignés pour donner la même molécule.

A19.3.10

Le complexe ne possède aucun électron non apparié. Le complexe ne possède aucun isomère géométrique, mais l'image miroir n'est pas superposable, il possède donc un isomère optique.

Q19.3.11

Vous attendriez-vous à ce que le Mg ₃ [Cr (CN) ₆] ₂ soit diamagnétique ou paramagnétique ? Expliquez votre raisonnement.

S19.3.11

La première étape pour déterminer le magnétisme du complexe consiste à calculer l'état d'oxydation du métal de transition. Dans ce cas, le métal de transition est le Cr.

Avant cela, nous devons déterminer la charge de l'ion complexe [Cr (CN) ₆] ₂ étant donné que l'état d'oxydation du Mg _{3 est de 2+. En utilisant les indices de l'$\displaystyle Mg^{2+}$ion et du} _{complexe [Cr (CN) ₆] 2, nous trouvons que l'état d'oxydation du} [Cr (CN) ₆] _{2, x, est :}

_{$\displaystyle 3(+2)+2(x)=0$}

_{$\displaystyle x=3$}

_{Maintenant que nous avons trouvé la charge du complexe de coordination, nous pouvons trouver la charge du métal de transition Cr étant donné que la charge de CN est -1. Encore une fois, en utilisant les indices, nous trouvons que l'état d'oxydation du Cr, y est :}

_{$\displaystyle y + 6(-1)=-3$}

_{$\displaystyle y=3$}

_{Par conséquent, l'état d'oxydation du métal de transition Cr est$\displaystyle Cr^{3+}$}

_{Ensuite, en utilisant le métal de transition$\displaystyle Cr^{3+}$ et le tableau périodique comme référence, nous pouvons déterminer la configuration électronique de$\displaystyle Cr^{3+}$ to be$\displaystyle [Ar]d^{3}$. Cela signifie qu'il y$\displaystyle Cr^{3+}$ a 3 électrons non appariés dans le sous-niveau 3D. Par conséquent, nous constatons qu'étant donné qu'au moins un électron n'est pas apparié (dans ce cas, les 3 électrons ne sont pas appariés),} le Mg ₃ [Cr (CN) ₆] _{2 est paramagnétique.}

A19.3.11

a) Paramagnétique

Q19.3.12

Vous attendez-vous à ce que les sels de l'ion or, Au ⁺, soient colorés ? Expliquez.

S19.3.12

Non. Les ions colorés ont des électrons non appariés sur leur orbite la plus éloignée. Une orbitale d partiellement remplie, par exemple, peut produire différentes couleurs. Une fois la configuration des gaz rares terminée, nous voyons que Au ⁺ a une configuration de [Xe] 4f ¹⁴ 5d ¹⁰. Comme Au ⁺ a un sous-niveau d complètement rempli, nous sommes certains que tous les sels de l'ion or, Au ⁺, seront incolores.

*Le cuivre (II) est un exemple d'ion coloré. Le Cu ²⁺ a une configuration électronique de [Ar] 3d ⁹. Il possède un électron non apparié. Le cuivre (II) apparaît en bleu.

A19.3.12

Non. Au ⁺ possède un sous-niveau 5 d complet.

Q19.3.13

[CuCl ₄] ²⁻ est vert. [Cu (H ₂ O) ₆] ²⁺ est bleu. Qui absorbe les photons de plus haute énergie ? Lequel devrait avoir une plus grande division du champ cristallin ?

S19.3.13

Bien qu'une couleur puisse apparaître d'une certaine manière, elle absorbe en fait une couleur différente, à l'opposé de celle-ci sur la roue chromatique.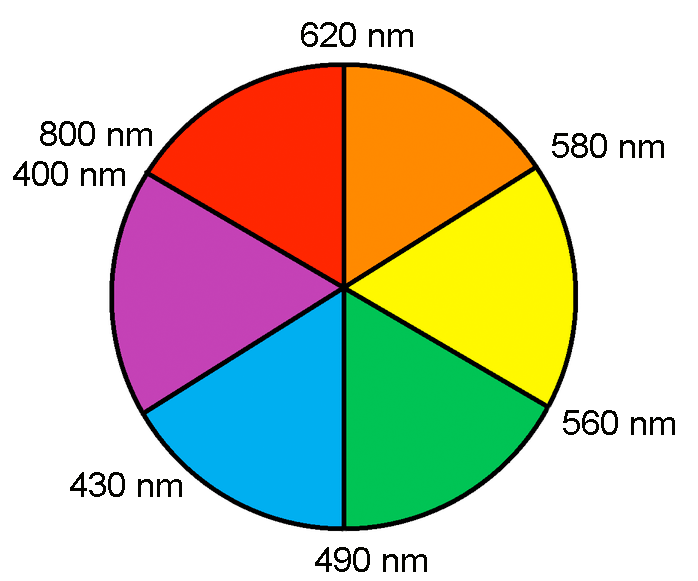

Dans ce cas ;

Le [CuCl ₄] ^2- apparaît en vert mais est opposé au rouge sur la roue chromatique qui est absorbée et se caractérise par des longueurs d'onde de 620 à 800 nanomètres.

Le [Cu (H ₂ O) ₆] ²⁺ apparaît en bleu mais est opposé à l'orange sur la roue chromatique qui est absorbée et se caractérise par des longueurs d'onde de 580 à 620 nanomètres.

Pour déterminer lequel absorbe les photons les plus énergétiques, il faut examiner le complexe lui-même. Une énergie plus élevée indique un photon de haute énergie absorbé et une énergie plus faible indique un photon de faible énergie absorbé. Comment pouvons-nous le déterminer ? En examinant le complexe et plus particulièrement le ligand attaché et sa localisation dans la série spectrochimique.

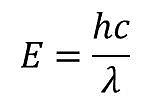
Les ligands attachés sont l'eau et le chlore et comme l'eau est un ligand plus fort que le chlore selon la série, elle possède également une énergie plus importante, ce qui indique une énergie plus élevée. Cela signifie que le complexe [Cu (H ₂ O) ₆] ²⁺ absorbe un photon d'énergie plus élevée en raison de son ligand plus fort que le chlore.

La deuxième partie de cette question demande également quel complexe devrait avoir une division du champ cristallin plus importante. Pour le déterminer, vous utilisez également la série spectrochimique et déterminez quel ligand est le plus fort. Puisque le H ₂ O est plus fort que le Cl ^- sur la série spectrochimique, on peut dire que le [Cu (H ₂ O) ₆] ²⁺ possède une division du champ cristallin plus élevée.

A19.3.13

a) [Cu (H ₂ O) ₆] ²⁺

^b) [Cu (H ₂ O) ₆] ²⁺ présente une division du champ cristallin plus élevée