10.6 : Structures en treillis dans les solides cristallins
- Page ID
- 193920
- Décrire la disposition des atomes et des ions dans les structures cristallines
- Calculer les rayons ioniques à l'aide des dimensions unitaires
- Expliquer l'utilisation des mesures de diffraction des rayons X pour déterminer les structures cristallines
Plus de 90 % des solides naturels et artificiels sont cristallins. La plupart des solides se forment avec un arrangement régulier de leurs particules, car les interactions attrayantes entre les particules sont maximisées et l'énergie intermoléculaire totale est minimisée, lorsque les particules se regroupent de la manière la plus efficace. L'arrangement régulier au niveau atomique se reflète souvent au niveau macroscopique. Dans ce module, nous allons explorer certains détails concernant les structures des solides cristallins métalliques et ioniques et apprendre comment ces structures sont déterminées expérimentalement.
Les structures des métaux
Nous commencerons notre discussion sur les solides cristallins en examinant les métaux élémentaires, qui sont relativement simples car chacun ne contient qu'un seul type d'atome. Un métal pur est un solide cristallin dont les atomes métalliques sont étroitement liés les uns aux autres selon un schéma répétitif. Certaines des propriétés des métaux en général, telles que leur malléabilité et leur ductilité, sont dues en grande partie au fait que des atomes identiques sont disposés selon un schéma régulier. Les propriétés différentes d'un métal par rapport à un autre dépendent en partie de la taille de leurs atomes et des spécificités de leurs arrangements spatiaux. Nous explorerons les similitudes et les différences entre quatre des géométries de cristaux métalliques les plus courantes dans les sections qui suivent.
Cellules unitaires des métaux
La structure d'un solide cristallin, qu'il s'agisse d'un métal ou non, est mieux décrite en considérant son unité répétitive la plus simple, appelée cellule unitaire. La cellule unitaire est constituée de points de réseau qui représentent les emplacements des atomes ou des ions. L'ensemble de la structure est alors constitué de cette cellule unitaire se répétant en trois dimensions, comme illustré à la figure\(\PageIndex{1}\).
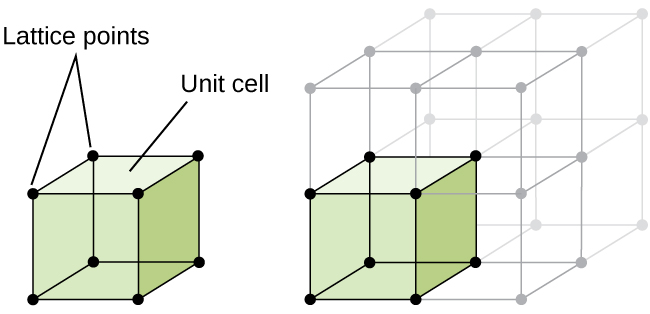
Commençons notre étude de la structure du réseau cristallin et des cellules unitaires avec la structure la plus simple et la cellule unitaire la plus élémentaire. Pour visualiser cela, imaginez prendre un grand nombre de sphères identiques, telles que des balles de tennis, et les disposer uniformément dans un contenant. La méthode la plus simple consiste à créer des couches dans lesquelles les sphères d'une couche sont directement au-dessus de celles de la couche inférieure, comme illustré sur la figure\(\PageIndex{2}\). Cette disposition est appelée structure cubique simple, et la cellule unitaire est appelée cellule unitaire cubique simple ou cellule unitaire cubique primitive.
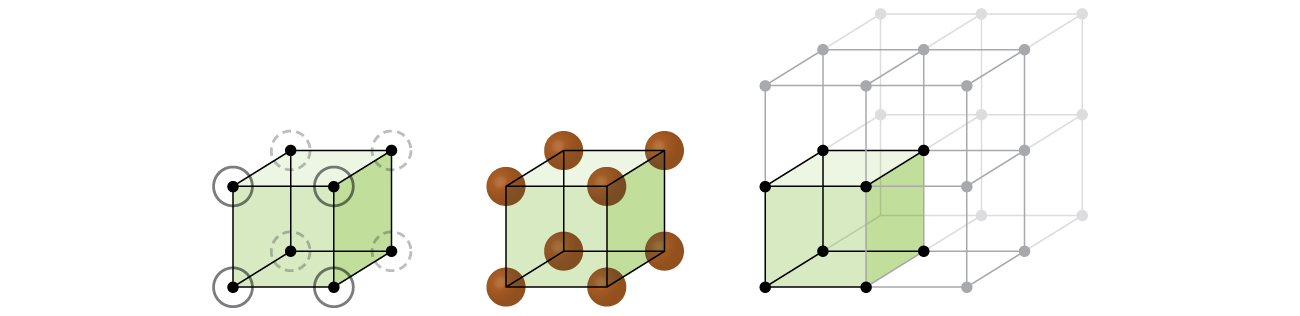
Dans une structure cubique simple, les sphères ne sont pas emballées aussi étroitement qu'elles pourraient l'être et elles ne « remplissent » qu'environ 52 % du volume du contenant. Il s'agit d'une disposition relativement inefficace, et un seul métal (polonium, Po) cristallise dans une structure cubique simple. Comme le montre la figure\(\PageIndex{3}\), un solide avec ce type d'arrangement est constitué de plans (ou couches) dans lesquels chaque atome entre en contact uniquement avec les quatre voisins les plus proches de sa couche ; un atome directement au-dessus dans la couche supérieure ; et un atome directement en dessous dans la couche inférieure. Le nombre d'autres particules avec lesquelles chaque particule d'un solide cristallin entre en contact est connu sous le nom de numéro de coordination. Pour un atome de polonium dans un réseau cubique simple, le nombre de coordination est donc de six.
 « height="200" width="463 » src= »/@api /deki/files/61021/CNX_Chem_10_06_SimpleCub2.jpg « >
« height="200" width="463 » src= »/@api /deki/files/61021/CNX_Chem_10_06_SimpleCub2.jpg « >
Dans un réseau cubique simple, la cellule unitaire qui se répète dans toutes les directions est un cube défini par les centres de huit atomes, comme le montre la figure\(\PageIndex{4}\). Les atomes situés aux angles adjacents de cette cellule unitaire entrent en contact les uns avec les autres, de sorte que la longueur du bord de cette cellule est égale à deux rayons atomiques, soit un diamètre atomique. Une cellule unitaire cubique ne contient que les parties de ces atomes qui s'y trouvent. Comme un atome situé à l'angle d'une cellule unitaire cubique simple est contenu dans un total de huit cellules unitaires, seul un huitième de cet atome se trouve dans une cellule unitaire spécifique. Et comme chaque cellule d'unité cubique simple possède un atome à chacun de ses huit « coins », il y a un\(8×\dfrac{1}{8}=1\) atome dans une cellule d'unité cubique simple.
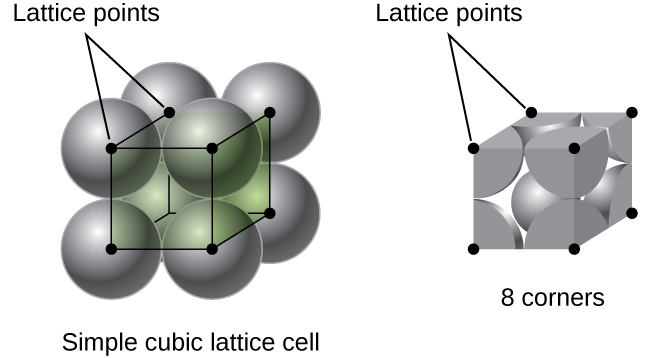
La longueur du bord de la cellule unitaire de l'alpha-polonium est de 336pm.
- Détermine le rayon d'un atome de polonium.
- Déterminez la densité de l'alpha-polonium.
Solution
L'alpha polonium cristallise dans une cellule unitaire cubique simple :

(a) Deux atomes de Po adjacents entrent en contact l'un avec l'autre, de sorte que la longueur du bord de cette cellule est égale à deux rayons atomiques de Po :\(l = 2r\). Par conséquent, le rayon de Po est
\[r=\mathrm{\dfrac{l}{2}=\dfrac{336\: pm}{2}=168\: pm}\nonumber \]
(b) La densité est donnée par
\[\mathrm{density=\dfrac{mass}{volume}}.\nonumber \]
La densité du polonium peut être déterminée en déterminant la densité de sa cellule unitaire (la masse contenue dans une cellule unitaire divisée par le volume de la cellule unitaire). Comme une cellule unitaire Po contient un huitième d'atome de Po à chacun de ses huit coins, une cellule unitaire contient un atome de Po.
La masse d'une cellule unitaire Po peut être déterminée par :
\[\mathrm{1\: Po\: unit\: cell×\dfrac{1\: Po\: atom}{1\: Po\: unit\: cell}×\dfrac{1\: mol\: Po}{6.022\times 10^{23}\:Po\: atoms}×\dfrac{208.998\:g}{1\: mol\: Po}=3.47\times 10^{−22}\:g}\nonumber \]
Le volume d'une cellule unitaire Po peut être déterminé par :
\[V=l^3=\mathrm{(336\times 10^{−10}\:cm)^3=3.79\times 10^{−23}\:cm^3}\nonumber \]
(Notez que la longueur du bord a été convertie de pm en cm pour obtenir les unités de volume habituelles pour la densité.)
Par conséquent, la densité de
\[\mathrm{Po=\dfrac{3.471\times 10^{−22}\:g}{3.79\times 10^{−23}\:cm^3}=9.16\: g/cm^3}\nonumber \]
La longueur du bord de la cellule unitaire pour le nickel est de 0,3524 nm. La densité du Ni est de 8,90 g/cm 3. Le nickel cristallise-t-il dans une structure cubique simple ? Expliquez.
- Réponse
-
Non Si Ni était un cubique simple, sa densité serait donnée par :
\[\mathrm{1\: Ni\: atom×\dfrac{1\: mol\: Ni}{6.022\times 10^{23}\:Ni\: atoms}×\dfrac{58.693\:g}{1\: mol\: Ni}=9.746\times 10^{−23}\:g}\nonumber \]
\[V=l^3=\mathrm{(3.524\times 10^{−8}\:cm)^3=4.376\times 10^{−23}\:cm^3}\nonumber \]
Alors la densité de Ni serait
\[(\mathrm{=\dfrac{9.746\times 10^{−23}\:g}{4.376\times 10^{−23}\:cm^3}=2.23\: g/cm^3}\nonumber \]
Comme la densité réelle du Ni n'est pas proche de celle-ci, le Ni ne forme pas une simple structure cubique.
La plupart des cristaux métalliques sont l'un des quatre principaux types de cellules unitaires. Pour l'instant, nous allons nous concentrer sur les trois cellules unitaires cubiques : la cellule cubique simple (que nous avons déjà vue), la cellule unitaire cubique centrée sur le corps et la cellule unitaire cubique centrée sur la face, qui sont toutes illustrées sur la figure\(\PageIndex{5}\). (Notez qu'il existe en fait sept systèmes de treillis différents, dont certains ont plus d'un type de réseau, pour un total de 14 types différents de cellules unitaires. Nous laisserons les géométries les plus complexes pour plus tard dans ce module.)

Certains métaux cristallisent dans un arrangement qui possède une cellule unitaire cubique avec des atomes à tous les coins et un atome au centre, comme le montre la figure\(\PageIndex{6}\). C'est ce que l'on appelle un solide cubique centré sur le corps (BCC). Les atomes situés dans les coins d'une cellule unitaire BCC ne sont pas en contact les uns avec les autres mais entrent en contact avec l'atome situé au centre. Une cellule unitaire BCC contient deux atomes : un huitième d'atome à chacun des huit coins (\(8×\dfrac{1}{8}=1\)atome depuis les coins) plus un atome depuis le centre. Tout atome de cette structure touche quatre atomes dans la couche supérieure et quatre atomes dans la couche inférieure. Ainsi, un atome dans une structure BCC a un numéro de coordination de huit.
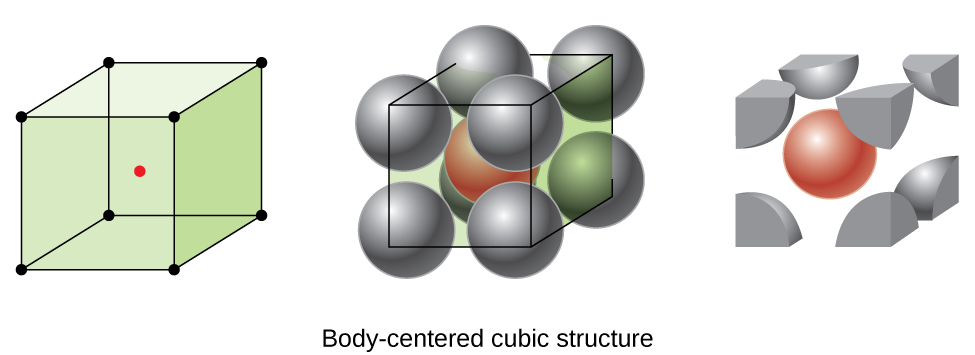
Les atomes dans les arrangements BCC sont emballés beaucoup plus efficacement que dans une structure cubique simple, occupant environ 68 % du volume total. Les métaux isomorphes à structure BCC comprennent le K, le Ba, le Cr, le Mo, le W et le Fe à température ambiante. (Les éléments ou composés qui cristallisent avec la même structure sont considérés comme isomorphes.)
De nombreux autres métaux, tels que l'aluminium, le cuivre et le plomb, cristallisent dans un arrangement comportant une cellule unitaire cubique avec des atomes à tous les coins et au centre de chaque face, comme illustré sur la figure\(\PageIndex{7}\). Cet arrangement est appelé solide cubique à face centrée (FCC). Une cellule unitaire FCC contient quatre atomes : un huitième d'atome à chacun des huit coins (\(8×\dfrac{1}{8}=1\)atome depuis les coins) et un demi-atome sur chacune des six faces (\(6×\dfrac{1}{2}=3\)atomes provenant des faces). Les atomes situés aux angles touchent les atomes situés au centre des faces adjacentes le long des diagonales des faces du cube. Comme les atomes se trouvent sur des points de réseau identiques, ils ont des environnements identiques.
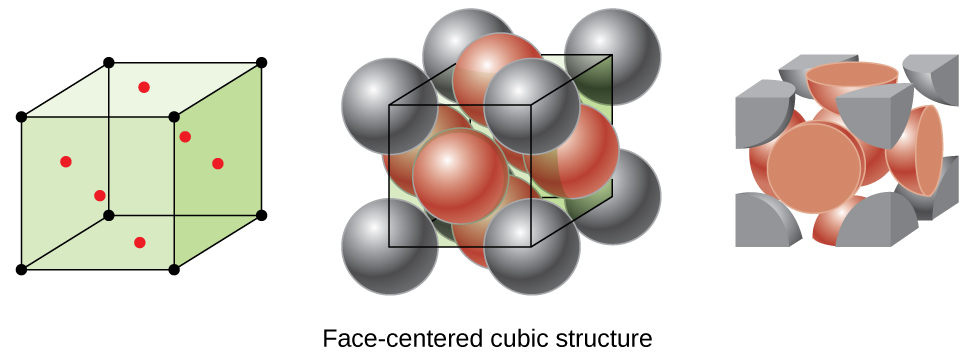
Les atomes d'un arrangement FCC sont regroupés le plus étroitement possible, les atomes occupant 74 % du volume. Cette structure est également appelée emballage cubique le plus proche (CCP). Dans le CCP, il existe trois couches répétitives d'atomes disposés de manière hexagonale. Chaque atome entre en contact avec six atomes dans sa propre couche, trois dans la couche supérieure et trois dans la couche inférieure. Dans cet arrangement, chaque atome touche 12 voisins proches et possède donc un numéro de coordination de 12. Le fait que les arrangements FCC et CCP soient équivalents n'est peut-être pas immédiatement évident, mais la raison pour laquelle ils sont en fait la même structure est illustrée dans la figure\(\PageIndex{8}\).
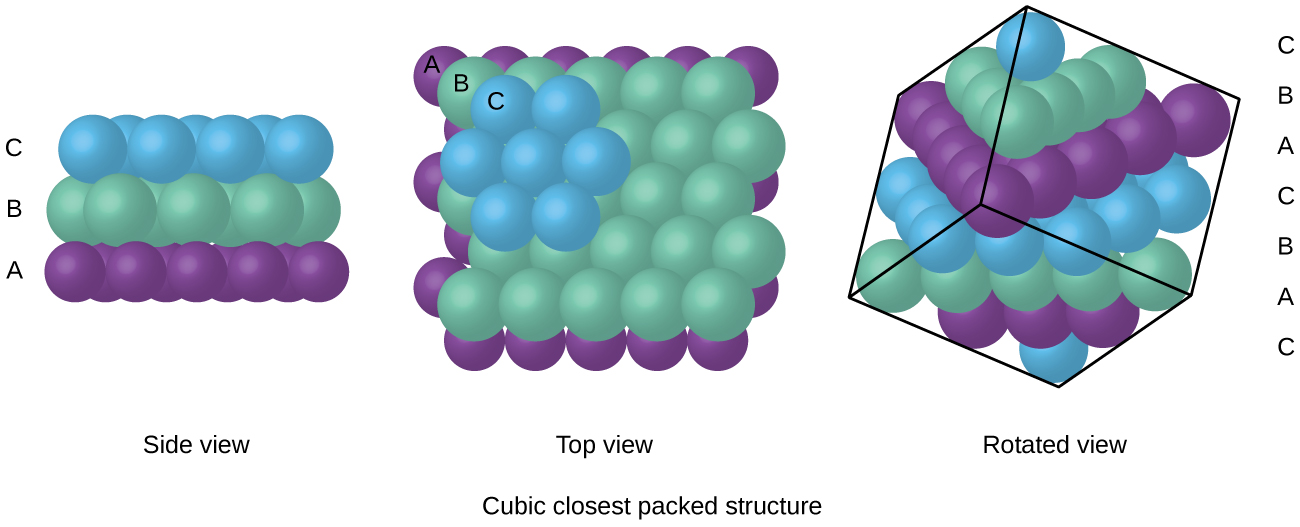
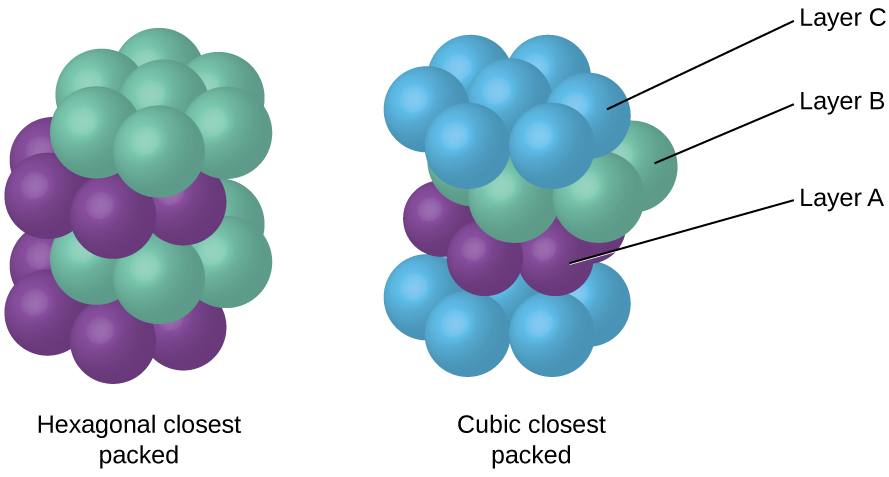
Parce que l'assemblage plus serré maximise les attractions globales entre les atomes et minimise l'énergie intermoléculaire totale, les atomes de la plupart des métaux se regroupent de cette manière. Nous trouvons deux types de garnissage le plus proche dans des structures cristallines métalliques simples : le CCP, que nous avons déjà rencontré, et le conditionnement le plus proche hexagonal (HCP) illustré sur la figure\(\PageIndex{9}\). Les deux sont constitués de couches répétées d'atomes disposés de manière hexagonale. Dans les deux types, une deuxième couche (B) est placée sur la première couche (A) de telle sorte que chaque atome de la deuxième couche soit en contact avec trois atomes de la première couche. La troisième couche est positionnée de deux manières. Dans le HCP, les atomes de la troisième couche sont directement au-dessus des atomes de la première couche (c'est-à-dire que la troisième couche est également de type A), et l'empilement consiste en une alternance de couches serrées de type A et de type B (c'est-à-dire ABABAB). Dans le CCP, les atomes de la troisième couche ne sont pas au-dessus des atomes de l'une ou l'autre des deux premières couches (c'est-à-dire que la troisième couche est de type C), et l'empilement consiste en une alternance de couches serrées de type A, de type B et de type C (c'est-à-dire ABCABCABC). Environ les deux tiers de tous les métaux cristallisent dans les réseaux les plus serrés avec un nombre de coordination de 12. Les métaux qui cristallisent dans une structure HCP incluent Cd, Co, Li, Mg, Na et Zn, et les métaux qui cristallisent dans une structure CCP incluent Ag, Al, Ca, Cu, Ni, Pb et Pt.
Le calcium cristallise dans une structure cubique à faces centrées. La longueur du bord de sa cellule unitaire est de 558,8 pm.
- Quel est le rayon atomique du Ca dans cette structure ?
- Calculez la densité de Ca.
Solution
(a) Dans une structure FCC, les atomes de Ca entrent en contact les uns avec les autres sur la diagonale de la face, de sorte que la longueur de la diagonale est égale à quatre rayons atomiques de Ca (d = 4 r).
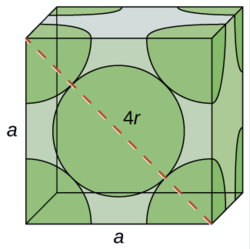
Deux arêtes adjacentes et la diagonale de la face forment un triangle droit, la longueur de chaque côté étant égale à 558,8 pm et la longueur de l'hypoténuse égale à quatre rayons atomiques de Ca :
\[\begin{align*} a^2+a^2 &=d^2 \\[4pt] \mathrm{(558.8\:pm)^2+(558.5\:pm)^2} &=(4r)^2 \end{align*} \nonumber \]
Résoudre ce problème donne
\[r=\mathrm{\sqrt{\dfrac{(558.8\:pm)^2+(558.5\:pm)^2}{16}}}=\textrm{197.6 pmg for a Ca radius}. \nonumber \]
(b) La densité est donnée par\(\mathrm{density=\dfrac{mass}{volume}}\). La densité du calcium peut être déterminée en déterminant la densité de sa cellule unitaire : par exemple, la masse contenue dans une cellule unitaire divisée par le volume de la cellule unitaire. Une cellule unitaire Ca centrée sur la face possède un huitième d'atome à chacun des huit coins (\(8 \times \dfrac{1}{8}=1\)atome) et un demi-atome sur chacune des six faces (\(6×\dfrac{1}{2}=3\)atomes), soit un total de quatre atomes dans la cellule unitaire.
La masse de la cellule unitaire peut être déterminée par :
\[\mathrm{1\: Ca\: unit\: cell×\dfrac{4\: Ca\: atoms}{1\: Ca\: unit\: cell}×\dfrac{1\: mol\: Ca}{6.022\times 10^{23}\:Ca\: atoms}×\dfrac{40.078\:g}{1\: mol\: Ca}=2.662\times 10^{−22}\:g} \nonumber \]
Le volume d'une cellule unitaire Ca peut être déterminé par :
\[V=a^3=\mathrm{(558.8\times 10^{−10}\:cm)^3=1.745\times 10^{−22}\:cm^3} \nonumber \]
(Notez que la longueur du bord a été convertie de pm en cm pour obtenir les unités de volume habituelles pour la densité.)
Ensuite, la densité du polonium :
\[\mathrm{Po=\dfrac{2.662\times 10^{−22}\:g}{1.745\times 10^{−22}\:cm^3}=1.53\: g/cm^3} \nonumber \]
L'argent cristallise dans une structure FCC. La longueur du bord de sa cellule unitaire est de 409pm.
- Quel est le rayon atomique de l'Ag dans cette structure ?
- Calculez la densité de Ag.
- Répondez à
-
14 h 44
- Réponse b
-
10,5 g/cm 3
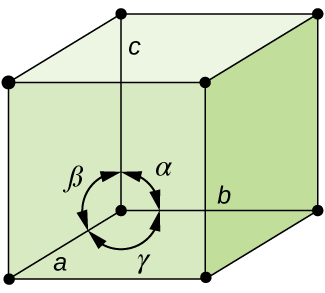
En général, une cellule unitaire est définie par la longueur de trois axes (a, b et c) et les angles (α, β et γ) entre eux, comme illustré à la figure\(\PageIndex{10}\). Les axes sont définis comme étant les longueurs entre les points du réseau spatial. Par conséquent, les axes des cellules unitaires joignent des points à des environnements identiques
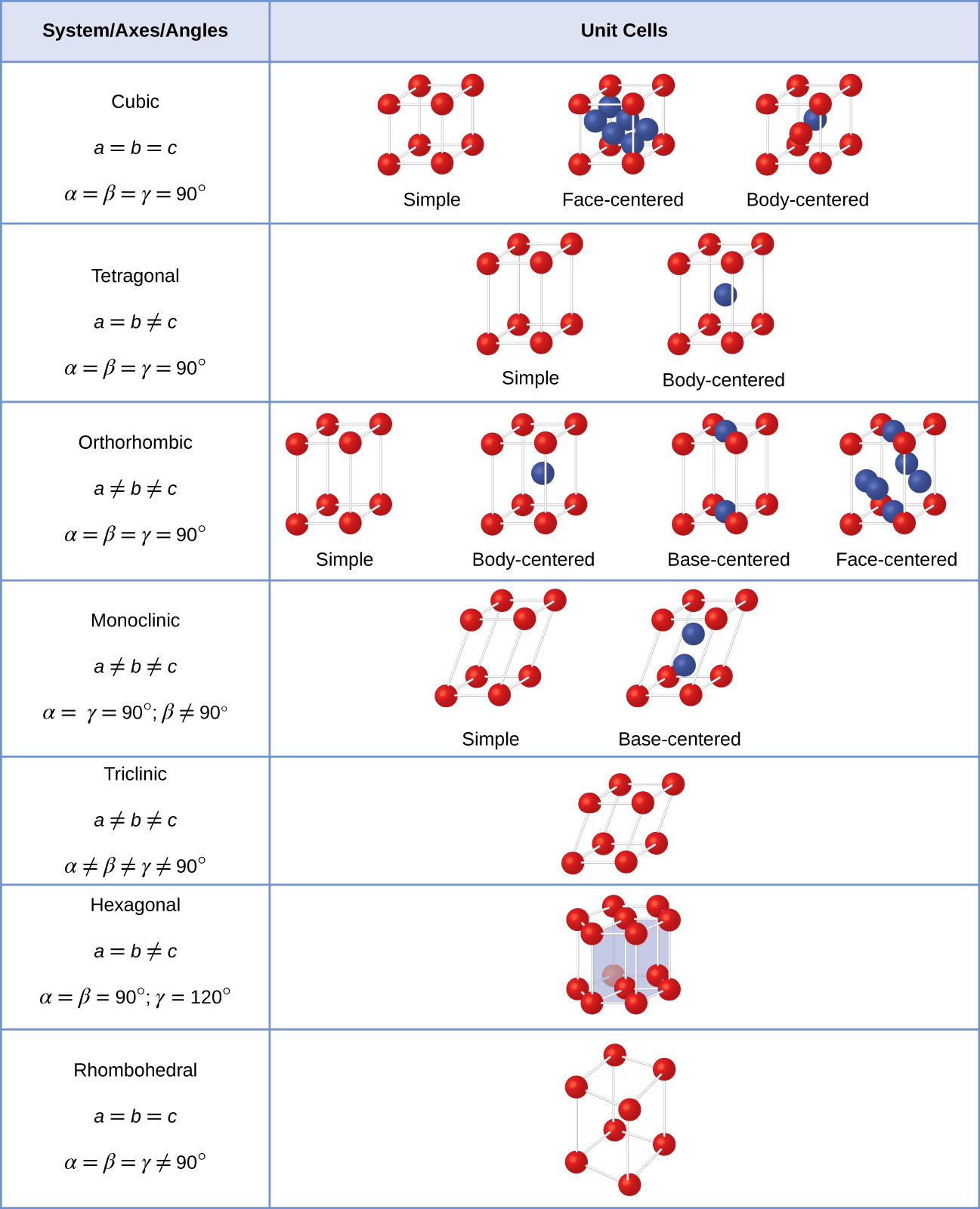
Il existe sept systèmes de treillis différents, dont certains ont plus d'un type de réseau, pour un total de quatorze cellules unitaires différentes, qui ont les formes illustrées sur la figure\(\PageIndex{11}\).
Les structures des cristaux ioniques
Les cristaux ioniques sont constitués de deux ou plusieurs types d'ions différents qui ont généralement des tailles différentes. La mise en place de ces ions dans une structure cristalline est plus complexe que celle d'atomes métalliques de même taille. La plupart des ions monatomiques se comportent comme des sphères chargées, et leur attraction pour les ions de charge opposée est la même dans toutes les directions. Par conséquent, les structures des composés ioniques sont stables (1) lorsque les ions d'une charge sont entourés par autant d'ions que possible de la charge opposée et (2) lorsque les cations et les anions sont en contact les uns avec les autres. Les structures sont déterminées par deux facteurs principaux : la taille relative des ions et le rapport entre le nombre d'ions positifs et négatifs dans le composé.
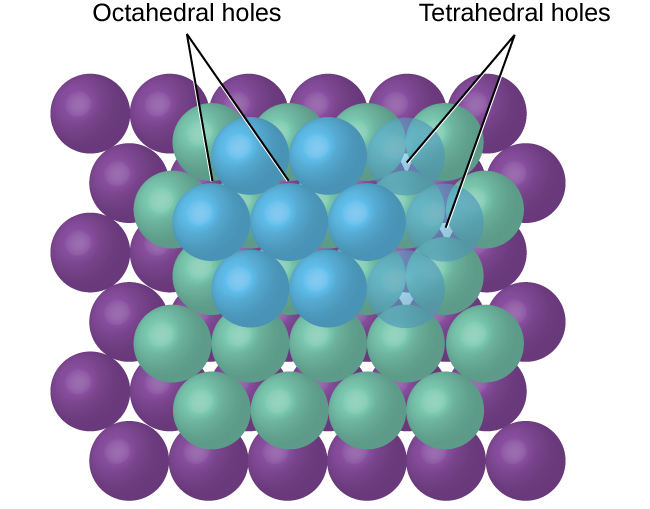
Dans les structures ioniques simples, nous trouvons généralement les anions, qui sont normalement plus gros que les cations, disposés en un réseau le plus serré. (Comme on l'a vu précédemment, des électrons supplémentaires attirés par le même noyau font grossir les anions et moins d'électrons attirés par le même noyau réduisent la taille des cations par rapport aux atomes à partir desquels ils sont formés.) Les plus petits cations occupent généralement l'un des deux types de trous (ou interstices) restant entre les anions. Le plus petit des trous se trouve entre trois anions dans un plan et un anion dans un plan adjacent. Les quatre anions qui entourent ce trou sont disposés aux coins d'un tétraèdre, de sorte que le trou est appelé trou tétraédrique. Le type de trou le plus grand se trouve au centre de six anions (trois dans une couche et trois dans une couche adjacente) situés aux coins d'un octaèdre ; c'est ce que l'on appelle un trou octaédrique. La figure\(\PageIndex{12}\) illustre ces deux types de trous.
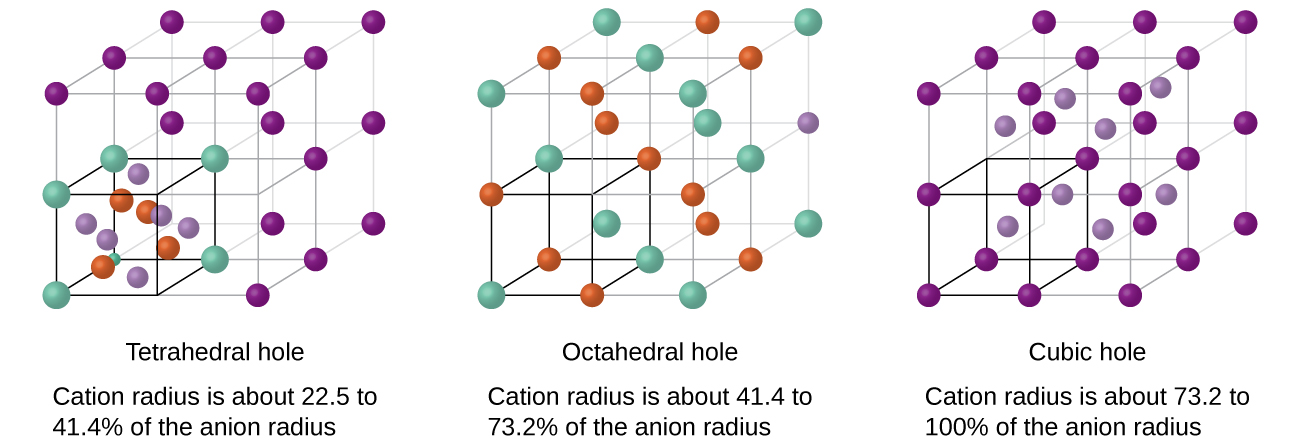
En fonction de la taille relative des cations et des anions, les cations d'un composé ionique peuvent occuper des trous tétraédriques ou octaédriques, comme illustré sur la figure\(\PageIndex{13}\). Des cations relativement petits occupent des trous tétraédriques, tandis que des cations plus gros occupent des trous octaédriques. Si les cations sont trop gros pour rentrer dans les trous octaédriques, les anions peuvent adopter une structure plus ouverte, telle qu'un simple réseau cubique. Les cations les plus gros peuvent alors occuper les plus grands trous cubiques rendus possibles par un espacement plus ouvert.
Il existe deux trous tétraédriques pour chaque anion dans un réseau d'anions HCP ou CCP. Un composé qui cristallise dans le réseau le plus compact d'anions avec des cations dans les trous tétraédriques peut avoir un rapport cation:anions maximal de 2:1 ; tous les trous tétraédriques sont remplis à ce rapport. Les exemples incluent le Li 2 O, le Na 2 O, le Li 2 S et le Na 2 S. Les composés dont le rapport est inférieur à 2:1 peuvent également cristalliser dans un réseau d'anions le plus compact avec des cations dans les trous tétraédriques, si les tailles ioniques conviennent. Dans ces composés, cependant, certains trous tétraédriques restent vacants.
Le sulfure de zinc est une source industrielle importante de zinc et est également utilisé comme pigment blanc dans la peinture. Le sulfure de zinc cristallise avec des ions zinc occupant la moitié des trous tétraédriques dans un réseau d'ions sulfure le plus compact. Quelle est la formule du sulfure de zinc ?
Solution
Comme il y a deux trous tétraédriques par anion (ion sulfure) et que la moitié de ces trous sont occupés par des ions zinc, il doit y avoir\(\dfrac{1}{2}×2\), soit 1, ion zinc par ion sulfure. Ainsi, la formule est ZnS.
Le séléniure de lithium peut être décrit comme le réseau le plus compact d'ions séléniure contenant des ions lithium dans tous les trous tétraédriques. Quelle est la formule du séléniure de lithium ?
- Réponse
-
\(\ce{Li2Se}\)
Le rapport entre les trous octaédriques et les anions dans une structure HCP ou CCP est de 1:1. Ainsi, les composés contenant des cations dans des trous octaédriques dans un réseau d'anions le plus serré peuvent avoir un rapport cation:anions maximal de 1:1. Dans le NiO, le MnS, le NaCl et le KH, par exemple, tous les trous octaédriques sont remplis. Des rapports inférieurs à 1:1 sont observés lorsque certains trous octaédriques restent vides.
L'oxyde d'aluminium cristallise avec les ions aluminium dans les deux tiers des trous octaédriques dans un réseau d'ions oxyde le plus compact. Quelle est la formule de l'oxyde d'aluminium ?
Solution
Comme il y a un trou octaédrique par anion (ion oxyde) et que seuls les deux tiers de ces trous sont occupés, le rapport entre l'aluminium et l'oxygène doit être de 1\(\dfrac{2}{3}\), ce qui donne.\(\mathrm{Al_{2/3}O}\) Le rapport des nombres entiers le plus simple est de 2:3, donc la formule est Al 2 O 3.
L'oxyde de titane à pigment blanc cristallise avec les ions titane dans la moitié des trous octaédriques dans un réseau d'ions oxyde le plus compact. Quelle est la formule de l'oxyde de titane ?
- Réponse
-
\(\ce{TiO2}\)
Dans un réseau cubique simple d'anions, il existe un trou cubique qui peut être occupé par un cation pour chaque anion du réseau. Dans le CsCl et dans d'autres composés ayant la même structure, tous les trous cubiques sont occupés. La moitié des trous cubiques sont occupés dans le SrH 2, l'UO 2, le SrCl 2 et le CaF 2.
Différents types de composés ioniques cristallisent souvent dans la même structure lorsque la taille relative de leurs ions et leur stœchiométrie (les deux principales caractéristiques qui déterminent la structure) sont similaires.
Cellules unités de composés ioniques
De nombreux composés ioniques cristallisent avec des cellules unitaires cubiques, et nous utiliserons ces composés pour décrire les caractéristiques générales des structures ioniques. Lorsqu'un composé ionique est composé de cations et d'anions de taille similaire dans un rapport 1:1, il forme généralement une structure cubique simple. Le chlorure de césium, CsCl, (Figure\(\PageIndex{14}\)) en est un exemple, avec Cs + et Cl − ayant des rayons de 174pm et 181pm, respectivement. Nous pouvons considérer cela comme des ions chlorure formant une simple cellule unitaire cubique, avec un ion césium au centre ; ou comme des ions césium formant une cellule unitaire avec un ion chlorure au centre ; ou comme de simples cellules unitaires cubiques formées par des ions Cs + chevauchant des cellules unitaires formées par des ions Cl −. Les ions césium et les ions chlorure se touchent le long des diagonales du corps des cellules unitaires. Un ion césium et un ion chlorure sont présents par unité de cellule, ce qui donne la stœchiométrie l:l requise par la formule du chlorure de césium. Notez qu'il n'y a pas de point de réseau au centre de la cellule et que CsCl n'est pas une structure BCC car un ion césium n'est pas identique à un ion chlorure.

Nous avons dit que l'emplacement des points de réseau est arbitraire. Ceci est illustré par une description alternative de la structure CsCl dans laquelle les points du réseau sont situés au centre des ions césium. Dans cette description, les ions césium sont situés sur les points du réseau aux coins de la cellule et l'ion chlorure est situé au centre de la cellule. Les deux cellules unitaires sont différentes, mais elles décrivent des structures identiques.
Lorsqu'un composé ionique est composé d'un rapport 1:1 de cations et d'anions dont la taille varie de manière significative, il cristallise généralement avec une cellule unitaire FCC, comme celle illustrée à la figure\(\PageIndex{15}\). Le chlorure de sodium, NaCl, en est un exemple, le Na + et le Cl − ayant des rayons de 102pm et 181pm, respectivement. Nous pouvons considérer cela comme des ions chlorure formant une cellule FCC, avec des ions sodium situés dans les trous octaédriques au milieu des bords de la cellule et au centre de la cellule. Les ions sodium et chlorure se touchent le long des bords des cellules. La cellule unitaire contient quatre ions sodium et quatre ions chlorure, ce qui donne la stœchiométrie 1:1 requise par la formule NaCl.

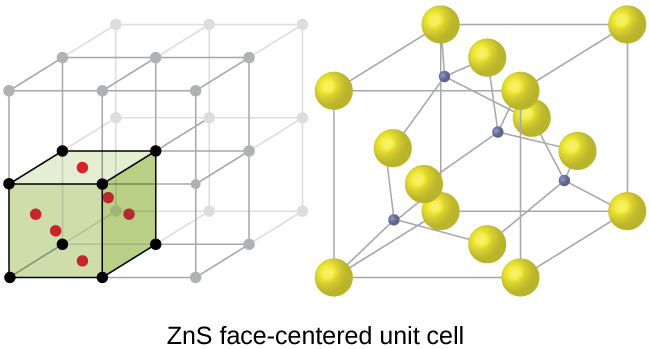
La forme cubique du sulfure de zinc, le mélange de zinc, cristallise également dans une cellule unitaire FCC, comme illustré à la figure\(\PageIndex{16}\). Cette structure contient des ions sulfure sur les points du réseau d'un réseau FCC. (La disposition des ions sulfure est identique à celle des ions chlorure dans le chlorure de sodium.) Le rayon d'un ion zinc ne représente qu'environ 40 % du rayon d'un ion sulfure, de sorte que ces petits ions Zn 2 + sont situés dans des trous tétraédriques alternés, c'est-à-dire dans la moitié des trous tétraédriques. Il y a quatre ions zinc et quatre ions sulfure dans la cellule unitaire, donnant la formule empirique ZnS.
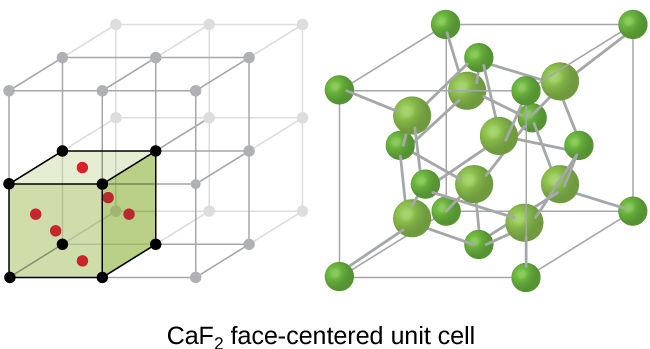
Une cellule unitaire de fluorure de calcium, telle que celle illustrée à la figure\(\PageIndex{17}\), est également une cellule unitaire FCC, mais dans ce cas, les cations sont situés sur les points du réseau ; les ions calcium équivalents sont situés sur les points du réseau d'un réseau FCC. Tous les sites tétraédriques du réseau d'ions calcium de la FCC sont occupés par des ions fluorure. Il y a quatre ions calcium et huit ions fluorure dans une cellule unitaire, ce qui donne un rapport calcium:fluor de 1:2, comme l'exige la formule chimique CaF 2. Un examen attentif de la figure\(\PageIndex{17}\) révélera un simple réseau cubique d'ions fluorure avec des ions calcium dans la moitié des trous cubiques. La structure ne peut pas être décrite en termes de réseau spatial de points sur les ions fluorure, car les ions fluorure n'ont pas tous des environnements identiques. L'orientation des quatre ions calcium par rapport aux ions fluorure est différente.
Calcul des rayons ioniques
Si nous connaissons la longueur des arêtes d'une cellule unitaire d'un composé ionique et la position des ions dans la cellule, nous pouvons calculer les rayons ioniques des ions contenus dans le composé en faisant des hypothèses sur les formes et les contacts ioniques individuels.
La longueur du bord de la cellule unitaire du LiCl (structure de type NaCl, FCC) est de 0,514 nm ou 5,14 Å. En supposant que l'ion lithium est suffisamment petit pour que les ions chlorure soient en contact, calculez le rayon ionique de l'ion chlorure. Remarque : L'unité de longueur angstrom, Å, est souvent utilisée pour représenter les dimensions à l'échelle atomique et équivaut à 10 −10 m.
Solution
Sur la face d'une cellule unitaire LiCl, les ions chlorure entrent en contact les uns avec les autres sur la diagonale de la face :
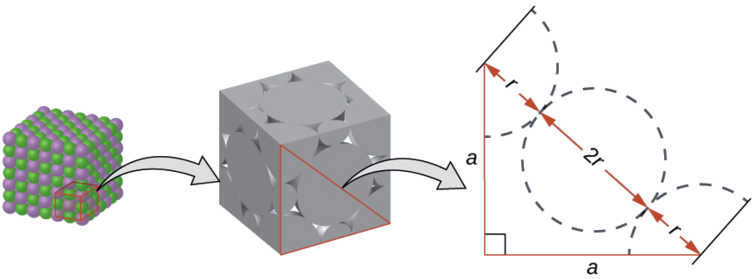
En traçant un triangle droit sur la face de la cellule unitaire, nous voyons que la longueur de la diagonale est égale à quatre rayons de chlorure (un rayon à partir de chaque angle de chlorure et un diamètre, ce qui équivaut à deux rayons, à partir de l'ion chlorure au centre de la face), donc\(d = 4r\). À partir du théorème de Pythagore, nous avons :
\[a^2+a^2=d^2 \nonumber \]
ce qui donne :
\[\mathrm{(0.514\:nm)^2+(0.514\:nm)^2}=(4r)^2=16r^2 \nonumber \]
La résolution de ce problème donne :
\[r=\mathrm{\sqrt{\dfrac{(0.514\:nm)^2+(0.514\:nm)^2}{16}}=0.182\: nm\:(1.82\: Å)\:for\: a\: Cl^−\: radius.} \nonumber \]
La longueur du bord de la cellule unitaire de KCl (structure de type NaCl, FCC) est de 6,28 Å. En supposant un contact anion-cation le long du bord de la cellule, calculez le rayon de l'ion potassium. Le rayon de l'ion chlorure est de 1,82 Å.
- Réponse
-
Le rayon de l'ion potassium est de 1,33 Å.
Il est important de comprendre que les valeurs des rayons ioniques calculées à partir des longueurs des arêtes des cellules unitaires dépendent de nombreuses hypothèses, telles que la forme sphérique parfaite pour les ions, qui sont au mieux des approximations. Ces valeurs calculées sont donc elles-mêmes approximatives et les comparaisons ne peuvent pas être poussées trop loin. Néanmoins, cette méthode s'est révélée utile pour calculer les rayons ioniques à partir de mesures expérimentales telles que les déterminations cristallographiques aux rayons X.
Cristallographie aux rayons X
La taille de la cellule unitaire et la disposition des atomes dans un cristal peuvent être déterminées à partir de mesures de la diffraction des rayons X par le cristal, appelées cristallographie aux rayons X. La diffraction est le changement de direction que subit une onde électromagnétique lorsqu'elle rencontre une barrière physique dont les dimensions sont comparables à celles de la longueur d'onde de la lumière. Les rayons X sont des rayonnements électromagnétiques dont les longueurs d'onde sont à peu près aussi longues que la distance entre les atomes voisins dans les cristaux (de l'ordre de quelques Å).
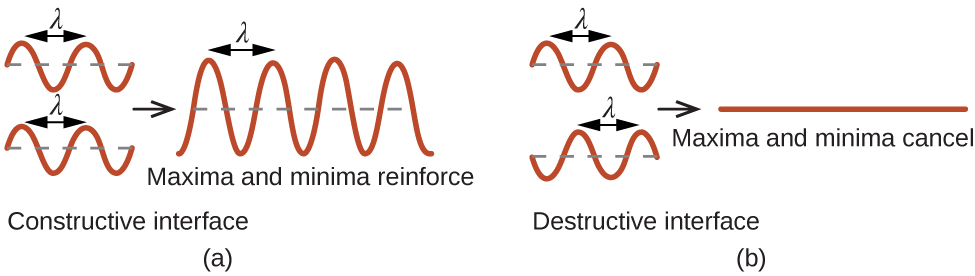
Lorsqu'un faisceau de rayons X monochromatiques frappe un cristal, ses rayons sont diffusés dans toutes les directions par les atomes du cristal. Lorsque des ondes diffusées se déplaçant dans la même direction se rencontrent, elles subissent des interférences, un processus par lequel les ondes se combinent pour produire une augmentation ou une diminution de l'amplitude (intensité) selon la mesure dans laquelle les maxima des ondes de combinaison sont séparés (Figure \(\PageIndex{18}\)).
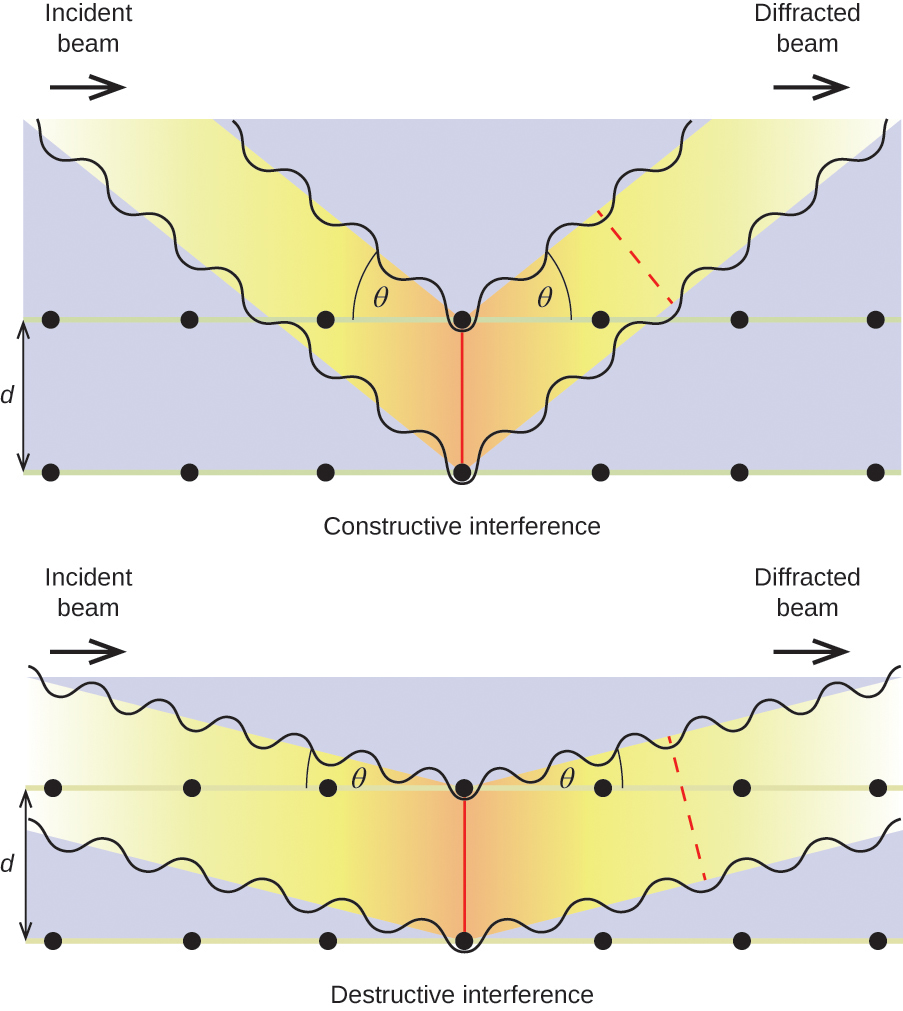
Lorsque des rayons X d'une certaine longueur d'onde, λ, sont diffusés par des atomes dans des plans cristallins adjacents séparés par une distance, d, ils peuvent subir une interférence constructive lorsque la différence entre les distances parcourues par les deux ondes avant leur combinaison est un facteur entier, n, de la longueur d'onde. Cette condition est satisfaite lorsque l'angle du faisceau diffracté, θ, est lié à la longueur d'onde et à la distance interatomique par l'équation suivante :
\[nλ=2d\sin \theta \label{Eq1} \]
Cette relation est connue sous le nom d'équation de Bragg en l'honneur de W. H. Bragg, le physicien anglais qui a expliqué ce phénomène pour la première fois. La figure\(\PageIndex{18}\) illustre deux exemples d'ondes diffractées provenant des deux mêmes plans cristallins. La figure de gauche représente des ondes diffractées à l'angle de Bragg, provoquant des interférences constructives, tandis que celle de droite montre la diffraction et un angle différent qui ne satisfait pas la condition de Bragg, ce qui entraîne une interférence destructrice.
Un diffractomètre à rayons X, tel que celui illustré sur la figure\(\PageIndex{20}\), peut être utilisé pour mesurer les angles auxquels les rayons X sont diffractés lorsqu'ils interagissent avec un cristal, comme décrit précédemment. À partir de ces mesures, l'équation de Bragg peut être utilisée pour calculer les distances entre les atomes, comme le montre l'exemple d'exercice suivant.

Dans un diffractomètre, des rayons X d'une longueur d'onde de 0,1315 nm ont été utilisés pour produire un diagramme de diffraction pour le cuivre. La diffraction du premier ordre (n = 1) s'est produite à un angle θ = 25,25°. Déterminez l'espacement entre les plans de diffraction dans le cuivre.
Solution
La distance entre les plans est déterminée en résolvant l'équation de Bragg (équation\(\ref{Eq1}\)) pour d.
Cela donne
\[d=\dfrac{nλ}{2\sinθ}=\mathrm{\dfrac{1(0.1315\:nm)}{2\sin(25.25°)}=0.154\: nm}\nonumber \]
Un cristal dont l'espacement entre les plans est égal à 0,394 nm diffracte des rayons X d'une longueur d'onde de 0,147 nm. Quel est l'angle de la diffraction du premier ordre ?
- Réponse
-
21,9°
La découverte de la structure de l'ADN en 1953 par Francis Crick et James Watson est l'une des grandes réussites de l'histoire des sciences. Ils ont reçu le prix Nobel de physiologie ou de médecine 1962, aux côtés de Maurice Wilkins, qui a fourni des preuves expérimentales de la structure de l'ADN. La chimiste britannique Rosalind Franklin a apporté une contribution inestimable à cette réalisation monumentale grâce à ses travaux de mesure des images de diffraction des rayons X de l'ADN. Au début de sa carrière, les recherches de Franklin sur la structure des charbons se sont révélées utiles à l'effort de guerre britannique. Après s'être concentrée sur les systèmes biologiques au début des années 1950, Franklin et le doctorant Raymond Gosling ont découvert que l'ADN se présente sous deux formes : une fibre longue et fine formée lorsqu'elle est humide (type « B ») et une fibre courte et large formée lors du séchage (type « A »). Ses images de l'ADN par diffraction aux rayons X ont fourni les informations cruciales qui ont permis à Watson et Crick de confirmer que l'ADN forme une double hélice et de déterminer les détails de sa taille et de sa structure. Franklin a également mené des recherches pionnières sur les virus et l'ARN qui contient leurs informations génétiques, révélant de nouvelles informations qui ont radicalement changé l'ensemble des connaissances dans le domaine. Après avoir développé un cancer de l'ovaire, Franklin a continué à travailler jusqu'à sa mort en 1958 à l'âge de 37 ans. Parmi les nombreuses reconnaissances posthumes de ses travaux, la Chicago Medical School of Finch University of Health Sciences a changé son nom pour devenir la Rosalind Franklin University of Medicine and Science en 2004, et a adopté une image de sa célèbre image de diffraction aux rayons X de l'ADN comme logo officiel de l'université.

Concepts clés et résumé
Les structures des métaux cristallins et des composés ioniques simples peuvent être décrites en termes de garnissage de sphères. Les atomes métalliques peuvent se regrouper dans des structures hexagonales les plus compactes, des structures cubiques les plus compactes, des structures centrées sur le corps et des structures cubiques simples. Les anions des structures ioniques simples adoptent généralement l'une de ces structures, et les cations occupent les espaces restants entre les anions. Les petits cations occupent généralement des trous tétraédriques dans le réseau d'anions le plus serré. Les cations les plus gros occupent généralement les trous octaédriques. Des cations encore plus gros peuvent occuper les trous cubiques d'un simple réseau cubique d'anions. La structure d'un solide peut être décrite en indiquant la taille et la forme d'une cellule unitaire ainsi que le contenu de la cellule. Le type de structure et les dimensions de la cellule unitaire peuvent être déterminés par des mesures de diffraction aux rayons X.
Lexique
- solide cubique centré sur le corps (BCC)
- structure cristalline comportant une cellule unitaire cubique avec des points de réseau aux coins et au centre de la cellule
- cellule unitaire cubique centrée sur le corps
- unité répétitive la plus simple d'un cristal cubique centré sur le corps ; c'est un cube contenant des points de réseau à chaque coin et au centre du cube
- Équation de Bragg
- équation qui met en relation les angles auxquels les rayons X sont diffractés par les atomes d'un cristal
- numéro de coordination
- nombre d'atomes les plus proches d'un atome donné dans un cristal ou de l'atome de métal central dans un complexe
- emballage cubique le plus proche (CCP)
- structure cristalline dans laquelle des plans d'atomes ou d'ions rapprochés sont empilés sous la forme d'une série de trois couches alternées d'orientations relatives différentes (ABC)
- diffraction
- redirection du rayonnement électromagnétique qui se produit lorsqu'il rencontre une barrière physique de dimensions appropriées
- solide cubique à face centrée (FCC)
- structure cristalline constituée d'une cellule unitaire cubique avec des points de réseau sur les angles et au centre de chaque face
- cellule unitaire cubique centrée sur la face
- unité répétitive la plus simple d'un cristal cubique centré sur une face ; c'est un cube contenant des points de réseau à chaque coin et au centre de chaque face
- emballage hexagonal le plus proche (HCP)
- structure cristalline dans laquelle des couches serrées d'atomes ou d'ions sont empilées sous la forme d'une série de deux couches alternées d'orientations relatives différentes (AB)
- trou
- (également, espace interstice) entre les atomes au sein d'un cristal
- isomorphe
- possédant la même structure cristalline
- trou octaédrique
- espace ouvert dans un cristal au centre de six particules situées aux angles d'un octaèdre
- cellule unitaire cubique simple
- (également, cellule unitaire cubique primitive) cellule unitaire dans la structure cubique simple
- structure cubique simple
- structure cristalline avec une cellule unitaire cubique avec des points de réseau uniquement aux angles
- réseau spatial
- tous les points d'un cristal ayant des environnements identiques
- trou tétraédrique
- espace tétraédrique formé par quatre atomes ou ions dans un cristal
- cellule unitaire
- la plus petite partie d'un réseau spatial qui est répétée en trois dimensions pour former l'ensemble du réseau
- Cristallographie aux rayons X
- technique expérimentale pour déterminer les distances entre les atomes d'un cristal en mesurant les angles auxquels les rayons X sont diffractés lorsqu'ils traversent le cristal


