1.6 : Traitement mathématique des résultats de mesure
- Page ID
- 194005
ting/3
- Expliquer l'approche de l'analyse dimensionnelle (étiquette factorielle) pour les calculs mathématiques impliquant des quantités.
- Décrire comment utiliser l'analyse dimensionnelle pour effectuer des conversions d'unités pour une propriété donnée et des calculs impliquant deux propriétés ou plus.
- Convertissez entre les trois unités de température principales : Fahrenheit, Celsius et Kelvin.
Il arrive souvent qu'une quantité d'intérêt ne soit pas facile (ou même possible) à mesurer directement, mais qu'elle doit plutôt être calculée à partir d'autres propriétés mesurées directement et de relations mathématiques appropriées. Par exemple, pensez à mesurer la vitesse moyenne d'un athlète qui court des sprints. Cela se fait généralement en mesurant le temps nécessaire à l'athlète pour courir de la ligne de départ à la ligne d'arrivée, ainsi que la distance entre ces deux lignes, puis en calculant la vitesse à partir de l'équation qui relie ces trois propriétés :
\[\mathrm{speed=\dfrac{distance}{time}} \nonumber \]
Un sprinter de qualité olympique peut courir 100 m en 10 s environ, ce qui correspond à une vitesse moyenne de
\[\mathrm{\dfrac{100\: m}{10\: s}=10\: m/s} \nonumber \]
Notez que cette arithmétique simple consiste à diviser les nombres de chaque quantité mesurée pour obtenir le numéro de la quantité calculée (100/10 = 10) et à diviser de la même manière les unités de chaque quantité mesurée pour obtenir l'unité de la quantité calculée (m/s = m/s). Maintenant, pensez à utiliser cette même relation pour prédire le temps nécessaire à une personne qui court à cette vitesse pour parcourir une distance de 25 m. La même relation entre les trois propriétés est utilisée, mais dans ce cas, les deux grandeurs fournies sont une vitesse (10 m/s) et une distance (25 m). Pour obtenir la propriété recherchée, le temps, l'équation doit être réorganisée de manière appropriée :
\[\mathrm{time=\dfrac{distance}{speed}} \nonumber \]
Le temps peut ensuite être calculé comme suit :
\[\mathrm{\dfrac{25\: m}{10\: m/s}=2.5\: s} \nonumber \]
Encore une fois, l'arithmétique des nombres (25/10 = 2,5) était accompagnée de la même arithmétique des unités (m/m/s = s) pour obtenir le nombre et l'unité du résultat, 2,5 s. Notez que, tout comme pour les nombres, lorsqu'une unité est divisée par une unité identique (dans ce cas, m/m), le résultat est « 1 », ou, comme on le dit couramment, les unités » annuler. »
Ces calculs sont des exemples d'une approche mathématique polyvalente connue sous le nom d'analyse dimensionnelle (ou méthode factorielle). L'analyse dimensionnelle repose sur cette prémisse : les unités de quantités doivent être soumises aux mêmes opérations mathématiques que les nombres qui leur sont associés. Cette méthode peut être appliquée à des calculs allant de simples conversions d'unités à des calculs plus complexes en plusieurs étapes impliquant plusieurs quantités différentes.
Facteurs de conversion et analyse dimensionnelle
Un rapport de deux quantités équivalentes exprimées avec des unités de mesure différentes peut être utilisé comme facteur de conversion d'unités. Par exemple, les longueurs de 2,54 cm et 1 pouce sont équivalentes (par définition), de sorte qu'un facteur de conversion unitaire peut être dérivé du rapport,
\[\mathrm{\dfrac{2.54\: cm}{1\: in.}\:(2.54\: cm=1\: in.)\: or\: 2.54\:\dfrac{cm}{in.}} \nonumber \]
Plusieurs autres facteurs de conversion couramment utilisés sont présentés dans le tableau\(\PageIndex{1}\).
| Longueur | Volume | Masse |
|---|---|---|
| 1 m = 1,0936 mètres | 1 L = 1,0567 pintes | 1 kg = 2,2046 livres |
| 1 po = 2,54 cm (exact) | 1 pinte = 0,94635 L | 1 livre = 453,59 g |
| 1 km = 0,62137 mi | 1 pied 3 = 28,317 L | 1 once (environ dupois) = 28,349 g |
| 1 km = 1609,3 m | 1 cuillère à soupe = 14,787 ml | 1 once (troy) = 31,103 g |
Lorsque nous multiplions une quantité (telle que la distance donnée en pouces) par un facteur de conversion d'unité approprié, nous convertissons la quantité en une valeur équivalente avec différentes unités (comme la distance en centimètres). Par exemple, le saut vertical de 34 pouces d'un joueur de basket-ball peut être converti en centimètres en :
\[\mathrm{34\: \cancel{in.} \times \dfrac{2.54\: cm}{1\:\cancel{in.}}=86\: cm} \nonumber \]
Comme cette simple arithmétique implique des quantités, le principe de l'analyse dimensionnelle exige que nous multipliions à la fois des nombres et des unités. Les nombres de ces deux quantités sont multipliés pour obtenir le numéro de la quantité de produit, 86, tandis que les unités sont multipliées pour obtenir
\[\mathrm{\dfrac{in.\times cm}{in.}}. \nonumber \]
Tout comme pour les nombres, un ratio d'unités identiques est également numériquement égal à un,
\[\mathrm{\dfrac{in.}{in.}=1} \nonumber \]
et le produit unitaire se simplifie ainsi en cm. (Lorsque des unités identiques se divisent pour obtenir un facteur de 1, on dit qu'elles « s'annulent ».) À l'aide de l'analyse dimensionnelle, nous pouvons déterminer qu'un facteur de conversion d'unités a été correctement configuré en vérifiant que l'unité d'origine sera annulée et que le résultat contiendra l'unité recherchée (convertie).
La masse d'un frisbee de compétition est de 125 g. Convertissez sa masse en onces à l'aide du facteur de conversion unitaire dérivé de la relation 1 oz = 28,349 g (Tableau\(\PageIndex{1}\)).
Solution
Si nous avons le facteur de conversion, nous pouvons déterminer la masse en kilogrammes à l'aide d'une équation similaire à celle utilisée pour convertir la longueur des pouces en centimètres.
\[x\:\mathrm{oz=125\: g\times unit\: conversion\: factor}\nonumber \]
Nous écrivons le facteur de conversion d'unités sous ses deux formes :
\[\mathrm{\dfrac{1\: oz}{28.349\: g}\:and\:\dfrac{28.349\: g}{1\: oz}}\nonumber \]
Le facteur de conversion d'unités correct est le ratio qui annule les unités de grammes et laisse les onces.
\ [\ begin {align*}
x \ : \ ce {oz} &= \ mathrm {125 \ : \ annuler {g} \ times \ dfrac {1 \ : oz} {28.349 \ : \ annuler {g}}} \ \
&= \ mathrm {\ left (\ dfrac {125} {28.349} \ right) \ :oz} \ \
&= \ mathrm {4.41 \ : oz \ : (trois \ : significatifs \ : chiffres)}
\ end {align*} \ nonumber \]
Convertissez un volume de 9,345 pintes en litres.
- Réponse
-
8 844 L
Au-delà des simples conversions d'unités, la méthode des étiquettes factorielles peut être utilisée pour résoudre des problèmes plus complexes impliquant des calculs. Quels que soient les détails, l'approche de base est la même : tous les facteurs impliqués dans le calcul doivent être orientés de manière appropriée pour garantir que leurs étiquettes (unités) s'annuleront et/ou se combineront de manière appropriée pour obtenir l'unité souhaitée dans le résultat. C'est pourquoi on parle de méthode d'étiquetage factoriel. Au fur et à mesure que votre étude de la chimie se poursuit, vous aurez de nombreuses occasions d'appliquer cette approche.
Quelle est la densité de l'antigel courant en unités de g/mL ? Un échantillon de 4 pintes d'antigel pèse 9,26 livres.
Solution
Puisque\(\mathrm{density=\dfrac{mass}{volume}}\), nous devons diviser la masse en grammes par le volume en millilitres. En général : le nombre d'unités de B = le nombre d'unités d'un facteur de conversion d'\(\times\)unités A. Les facteurs de conversion nécessaires sont donnés dans le tableau 1.7.1 : 1 lb = 453,59 g ; 1 L = 1,0567 pinte ; 1 L = 1 000 ml. Nous pouvons convertir la masse des livres en grammes en une seule étape :
\[\mathrm{9.26\:\cancel{lb}\times \dfrac{453.59\: g}{1\:\cancel{lb}}=4.20\times 10^3\:g}\nonumber \]
Nous devons utiliser deux étapes pour convertir le volume des pintes en millilitres.
- Convertissez les pintes en litres.
\[\mathrm{4.00\:\cancel{qt}\times\dfrac{1\: L}{1.0567\:\cancel{qt}}=3.78\: L}\nonumber \]
- Convertissez les litres en millilitres.
\[\mathrm{3.78\:\cancel{L}\times\dfrac{1000\: mL}{1\:\cancel{L}}=3.78\times10^3\:mL}\nonumber \]
Ensuite,
\[\mathrm{density=\dfrac{4.20\times10^3\:g}{3.78\times10^3\:mL}=1.11\: g/mL}\nonumber \]
Le calcul peut également être configuré de manière à utiliser trois facteurs de conversion d'unités de manière séquentielle, comme suit :
\[\mathrm{\dfrac{9.26\:\cancel{lb}}{4.00\:\cancel{qt}}\times\dfrac{453.59\: g}{1\:\cancel{lb}}\times\dfrac{1.0567\:\cancel{qt}}{1\:\cancel{L}}\times\dfrac{1\:\cancel{L}}{1000\: mL}=1.11\: g/mL}\nonumber \]
Quel est le volume en litres de 1 000 oz, étant donné que 1 L = 1,0567 pintes et 1 pinte = 32 oz (exactement) ?
- Réponse
-
\(\mathrm{2.956\times10^{-2}\:L}\)
Alors qu'elle est conduite de Philadelphie à Atlanta, sur une distance d'environ 1250 km, une Lamborghini Aventador Roadster 2014 utilise 213 litres d'essence.
- Quelle est la consommation de carburant (moyenne), en miles par gallon, enregistrée par le Roadster au cours de ce voyage ?
- Si l'essence coûte 3,80$ le gallon, quel était le coût du carburant pour ce voyage ?
Solution
(a) Nous convertissons d'abord la distance en kilomètres en miles :
\[\mathrm{1250\: km\times\dfrac{0.62137\: mi}{1\: km}=777\: mi}\nonumber \]
puis convertissez le volume de litres en gallons :
\[\mathrm{213\:\cancel{L}\times\dfrac{1.0567\:\cancel{qt}}{1\:\cancel{L}}\times\dfrac{1\: gal}{4\:\cancel{qt}}=56.3\: gal}\nonumber \]
Ensuite,
\[\mathrm{(average)\: mileage=\dfrac{777\: mi}{56.3\: gal}=13.8\: miles/gallon=13.8\: mpg}\nonumber \]
Le calcul peut également être configuré de manière à utiliser tous les facteurs de conversion de manière séquentielle, comme suit :
\[\mathrm{\dfrac{1250\:\cancel{km}}{213\:\cancel{L}}\times\dfrac{0.62137\: mi}{1\:\cancel{km}}\times\dfrac{1\:\cancel{L}}{1.0567\:\cancel{qt}}\times\dfrac{4\:\cancel{qt}}{1\: gal}=13.8\: mpg}\nonumber \]
(b) En utilisant le volume calculé précédemment en gallons, on trouve :
\[\mathrm{56.3\: gal\times\dfrac{$3.80}{1\: gal}=$214}\nonumber \]
Une Toyota Prius Hybrid utilise 59,7 L d'essence pour se déplacer de San Francisco à Seattle, soit une distance de 1 300 km (deux chiffres significatifs).
- Quelle consommation de carburant (moyenne), en miles par gallon, la Prius a-t-elle réalisée au cours de ce voyage ?
- Si l'essence coûte 3,90$ le gallon, quel était le coût du carburant pour ce voyage ?
- Répondez à une
-
51 mi/gal
- Réponse b
-
62$
Conversion des unités de température
Nous utilisons le mot température pour désigner la chaleur ou le froid d'une substance. L'un des moyens de mesurer un changement de température est d'utiliser le fait que la plupart des substances se dilatent lorsque leur température augmente et se contractent lorsque leur température diminue. Le mercure ou l'alcool d'un thermomètre en verre ordinaire change de volume à mesure que la température change. Comme le volume du liquide change plus que le volume du verre, nous pouvons voir le liquide se dilater lorsqu'il fait chaud et se contracter lorsqu'il fait froid.
Pour marquer une échelle sur un thermomètre, nous avons besoin d'un ensemble de valeurs de référence : deux des plus couramment utilisées sont les températures de congélation et d'ébullition de l'eau à une pression atmosphérique spécifiée. Sur l'échelle Celsius, 0 °C est définie comme la température de congélation de l'eau et 100 °C comme la température d'ébullition de l'eau. L'espace entre les deux températures est divisé en 100 intervalles égaux, que nous appelons degrés. Sur l'échelle Fahrenheit, le point de congélation de l'eau est défini à 32 °F et la température d'ébullition à 212 °F. L'espace entre ces deux points sur un thermomètre Fahrenheit est divisé en 180 parties égales (degrés).
La définition des échelles de température en degrés Celsius et Fahrenheit telle que décrite dans le paragraphe précédent aboutit à une relation légèrement plus complexe entre les valeurs de température sur ces deux échelles que pour différentes unités de mesure pour d'autres propriétés. La plupart des unités de mesure d'une propriété donnée sont directement proportionnelles les unes aux autres (y = mx). En utilisant des unités de longueur familières à titre d'exemple :
\[\mathrm{length\: in\: feet=\left(\dfrac{1\: ft}{12\: in.}\right)\times length\: in\: inches} \nonumber \]
où
- y = longueur en pieds,
- x = longueur en pouces, et
- la constante de proportionnalité, m, est le facteur de conversion.
Les échelles de température Celsius et Fahrenheit ne partagent toutefois pas de point zéro commun, de sorte que la relation entre ces deux échelles est linéaire plutôt que proportionnelle (\(y = mx + b\)). Par conséquent, la conversion d'une température d'une de ces échelles à l'autre nécessite plus qu'une simple multiplication par un facteur de conversion, m, elle doit également prendre en compte les différences entre les points zéro de l'échelle (\(b\)).
L'équation linéaire reliant les températures en degrés Celsius et Fahrenheit est facilement dérivée des deux températures utilisées pour définir chaque échelle. Si l'on représente la température Celsius\(x\) et la température Fahrenheit en tant que\(y\)\(m\), la pente est calculée comme suit :
\[\begin{align*} m &=\dfrac{\Delta y}{\Delta x} \\[4pt] &= \mathrm{\dfrac{212\: ^\circ F - 32\: ^\circ F}{100\: ^\circ C-0\: ^\circ C}} \\[4pt] &= \mathrm{\dfrac{180\: ^\circ F}{100\: ^\circ C}} \\[4pt] &= \mathrm{\dfrac{9\: ^\circ F}{5\: ^\circ C} }\end{align*} \nonumber \]
L'intersection y de l'équation, b, est ensuite calculée en utilisant l'une des paires de températures équivalentes, (100 °C, 212 °F) ou (0 °C, 32 °F), comme suit :
\[\begin{align*} b&=y-mx \\[4pt] &= \mathrm{32\:^\circ F-\dfrac{9\:^\circ F}{5\:^\circ C}\times0\:^\circ C} \\[4pt] &= \mathrm{32\:^\circ F} \end{align*} \nonumber \]
L'équation reliant les échelles de température est alors :
\[\mathrm{\mathit{T}_{^\circ F}=\left(\dfrac{9\:^\circ F}{5\:^\circ C}\times \mathit{T}_{^\circ C}\right)+32\:^\circ C} \nonumber \]
Une forme abrégée de cette équation qui omet les unités de mesure est la suivante :
\[\mathrm{\mathit{T}_{^\circ F}=\dfrac{9}{5}\times \mathit{T}_{^\circ C}+32} \nonumber \]
Le réarrangement de cette équation donne la forme utile pour convertir des degrés Fahrenheit en degrés Celsius :
\[\mathrm{\mathit{T}_{^\circ C}=\dfrac{5}{9}(\mathit{T}_{^\circ F}+32)} \nonumber \]
Comme indiqué précédemment dans ce chapitre, l'unité de température SI est le kelvin (K). Contrairement aux échelles Celsius et Fahrenheit, l'échelle kelvin est une échelle de température absolue dans laquelle 0 (zéro) K correspond à la température la plus basse qui peut théoriquement être atteinte. La découverte au début du XIXe siècle de la relation entre le volume d'un gaz et la température suggérait que le volume d'un gaz serait nul à −273,15 °C. En 1848, le physicien britannique William Thompson, qui a ensuite adopté le titre de Lord Kelvin, a proposé une échelle de température absolue basée sur ce concept (suite le traitement de ce sujet est fourni dans le chapitre de ce texte sur les gaz).
La température de congélation de l'eau sur cette échelle est de 273,15 K et sa température d'ébullition de 373,15 K. Notez que la différence numérique entre ces deux températures de référence est de 100, la même que pour l'échelle Celsius, et la relation linéaire entre ces deux échelles de température présentera donc une pente de\(\mathrm{1\:\dfrac{K}{^\circ\:C}}\). En suivant la même approche, les équations de conversion entre les échelles de température en kelvin et en degrés Celsius sont dérivées comme suit :
\[T_{\ce K}=T_{\mathrm{^\circ C}}+273.15 \nonumber \]
\[T_\mathrm{^\circ C}=T_{\ce K}-273.15 \nonumber \]
Le 273,15 de ces équations a été déterminé expérimentalement, il n'est donc pas exact. La figure\(\PageIndex{1}\) montre la relation entre les trois échelles de température. Rappelez-vous que nous n'utilisons pas le signe du degré avec des températures sur l'échelle des kelvins.
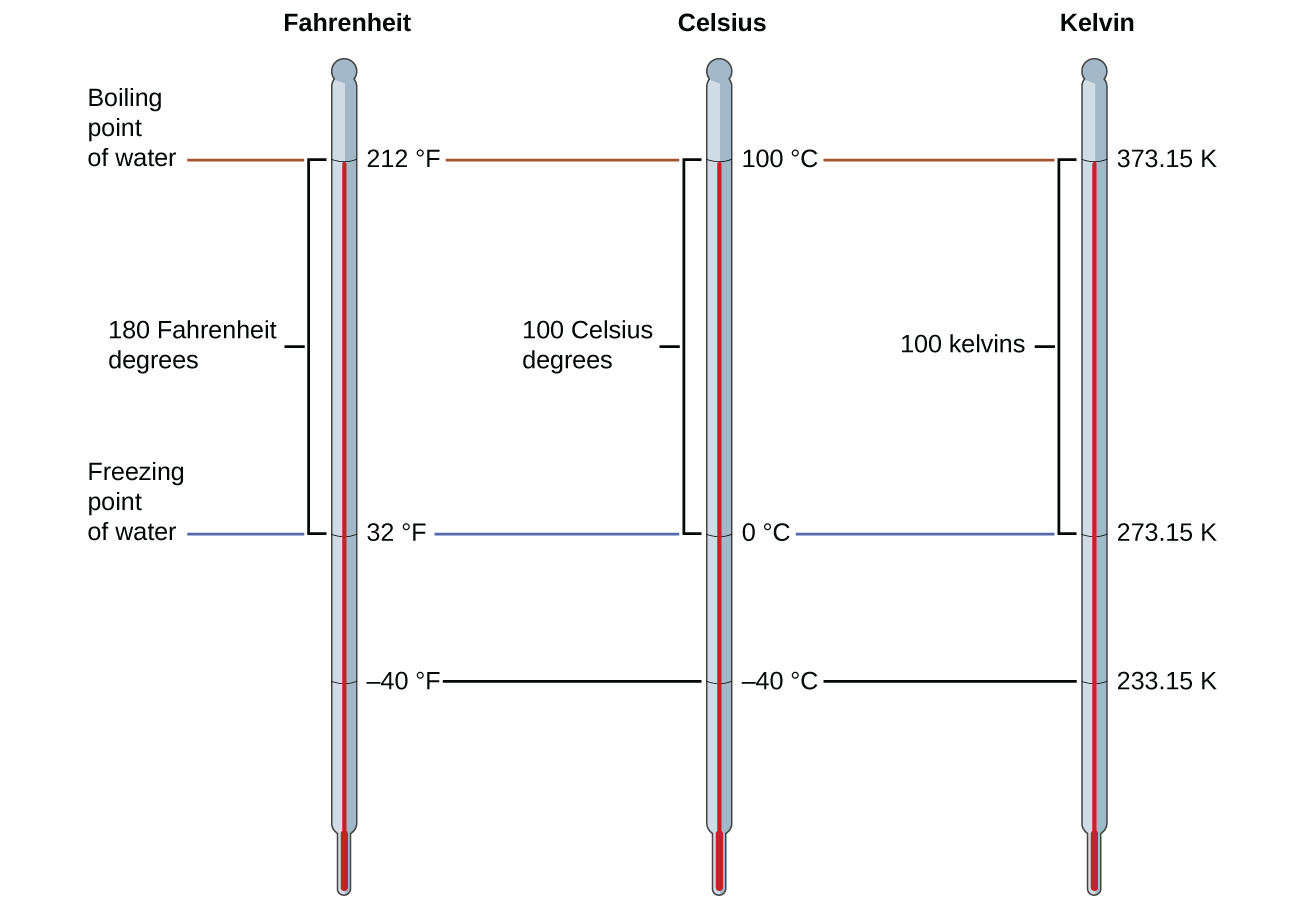
Bien que l'échelle de température en kelvin (absolue) soit l'échelle de température officielle du SI, le Celsius est couramment utilisé dans de nombreux contextes scientifiques et constitue l'échelle de choix pour les contextes non scientifiques dans presque toutes les régions du monde. Très peu de pays (les États-Unis et leurs territoires, les Bahamas, le Belize, les îles Caïmans et Palau) utilisent encore le Fahrenheit pour la météo, les médicaments et la cuisine.
La température corporelle normale est généralement acceptée comme étant de 37,0 °C (bien qu'elle varie en fonction de l'heure de la journée et de la méthode de mesure, ainsi que d'une personne à l'autre). Quelle est cette température sur l'échelle des kelvins et sur l'échelle des Fahrenheit ?
Solution
\[\mathrm{K= {^\circ C}+273.15=37.0+273.2=310.2\: K}\nonumber \]
\[\mathrm{^\circ F=\dfrac{9}{5}\:{^\circ C}+32.0=\left(\dfrac{9}{5}\times 37.0\right)+32.0=66.6+32.0=98.6\: ^\circ F}\nonumber \]
Convertir 80,92 °C en K et °F.
- Réponse
-
354,07 KG, 177,7 °F
La cuisson d'une pizza prête à l'emploi nécessite une température de four de 450 °F. Si vous êtes en Europe et que le thermomètre de votre four utilise l'échelle Celsius, quel est le réglage ? Quelle est la température en kelvins ?
Solution
\[\mathrm{^\circ C=\dfrac{5}{9}(^\circ F-32)=\dfrac{5}{9}(450-32)=\dfrac{5}{9}\times 418=232 ^\circ C\rightarrow set\: oven\: to\: 230 ^\circ C}\hspace{20px}\textrm{(two significant figures)}\nonumber \]
\[\mathrm{K={^\circ C}+273.15=230+273=503\: K\rightarrow 5.0\times 10^2\,K\hspace{20px}(two\: significant\: figures)}\nonumber \]
Convertir 50 °F en °C et K.
- Réponse
-
10 °C, 280 K
Résumé
Les mesures sont effectuées à l'aide de diverses unités. Il est souvent utile ou nécessaire de convertir une quantité mesurée d'une unité en une autre. Ces conversions sont effectuées à l'aide de facteurs de conversion unitaires, qui sont dérivés par de simples applications d'une approche mathématique appelée méthode facteur-étiquette ou analyse dimensionnelle. Cette stratégie est également utilisée pour calculer les quantités recherchées à l'aide de quantités mesurées et de relations mathématiques appropriées.
Équations clés
- \(T_\mathrm{^\circ C}=\dfrac{5}{9}\times T_\mathrm{^\circ F}-32\)
- \(T_\mathrm{^\circ F}=\dfrac{9}{5}\times T_\mathrm{^\circ C}+32\)
- \(T_\ce{K}={^\circ \ce C}+273.15\)
- \(T_\mathrm{^\circ C}=\ce K-273.15\)
Lexique
- analyse dimensionnelle
- (également, méthode facteur-étiquette) approche mathématique polyvalente qui peut être appliquée à des calculs allant de simples conversions d'unités à des calculs plus complexes en plusieurs étapes impliquant plusieurs quantités différentes
- Fahrenheit
- unité de température ; l'eau gèle à 32 °F et bout à 212 °F sur cette échelle
- facteur de conversion unitaire
- ratio de quantités équivalentes exprimées avec différentes unités ; utilisé pour convertir une unité en une unité différente


