10.3 : Inégalités rationnelles
- Page ID
- 165955
Pour résoudre les inégalités rationnelles, il faut trouver les zéros du numérateur et du dénominateur, puis utiliser ces valeurs pour étudier les régions de l'ensemble de solutions sur la ligne numérique.
Résolvez les inégalités et écrivez les ensembles de solutions en notation par intervalles :
- \(\dfrac{x − 1}{x + 1} ≥ 0\)
- \(\dfrac{2x − 3}{x + 1} ≤ 0\)
- \(\dfrac{x + 2}{x − 2} ≥ 0\)
Solution
- \(\begin{array} &&\dfrac{x − 1}{x + 1} ≥ 0 &\text{Example problem} \\ &\dfrac{x − 1}{x + 1} ≥ 0 &\text{The quotient must be greater than or equal to \(0\).} \ \ &x − 1 = 0, \ ; x = 1 & \ text {Trouve les zéros du numérateur} \ \ &x + 1 = 0, x = \ ; −1 & \ text {Trouve les zéros du dénominateur} \ end {array} \)
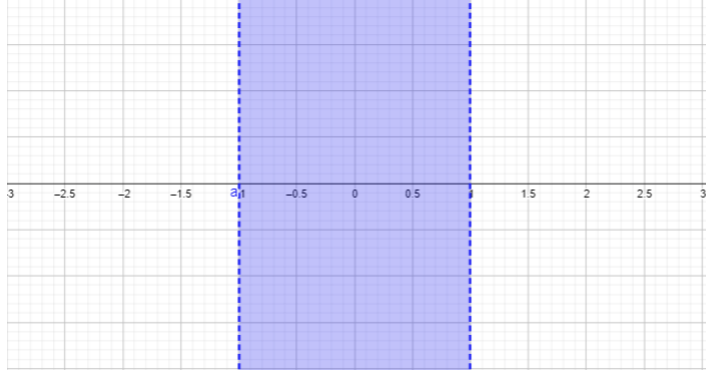
\(\begin{array} &&\text{For } x < −1, \text{ choose } x = −2. \;\;\dfrac{−2 − 1}{−2 + 1} = \dfrac{−3}{−1} = 3 ≥ 0 \\ &\text{Replacing \(-2\)pour les\(x\) résultats de la réponse\(3\), qui est supérieur ou égal à\(0\). Cette région\(x < −1\) est incluse dans l'ensemble de solutions.} \ \ [0,25 pouces] & \ text {Pour} −1 < x < 1, \ text {choose} x = 0. \ ; \ dfrac {0 − 1} {0 + 1} = \ dfrac {−1} {1} = −1 < 0 \ \ & \ text {Remplacer\(0\) pour\(x\) obtenir des résultats dans la réponse\(-1\), qui est inférieure à\(0\), non satisfaisante l'inégalité donnée dans le problème.} \ \ & \ text {Cette région\(−1 < x < 1\) est exclue de l'ensemble de solutions.} \ \ [0,25 in] & \ text {Pour} x > 1, \ text {choose} x = 2. \ ; \ ; \ dfrac {2 − 1} {2 + 1} = \ dfrac {1} {3} ≥ 0 \ \ & \ text {Remplacer\(2\) pour les\(x\) résultats de la réponse\(\dfrac{1}{3}\), qui est supérieur ou égal à\(0\). Cette région\(x > 1\) est incluse dans l'ensemble de solutions.} \ \ [0,25 pouce] & (−∞, −1) (1, ∞) \ \ & \ text {Réponse finale écrite en notation par intervalles (voir la section sur la notation par intervalles pour plus de détails).} \ end {tableau} \)
- \(\begin{array} &&\dfrac{2x − 3}{x + 1} ≤ 0 &\text{Example problem} \\ &\dfrac{2x − 3}{x + 1} ≤ 0 &\text{The quotient must be less than or equal to \(0\).} \ \ &2x − 3 = 0, \ ; x = 1,5 & \ text {Trouve les zéros du numérateur} \ \ &x + 1 = 0, \ ; x = −1 & \ text {Trouve les zéros du dénominateur} \ end {array} \)
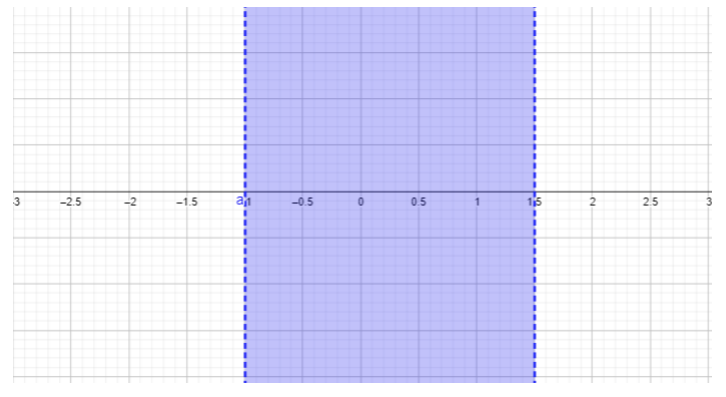
\(\begin{array} &&\text{For } x < −1, \text{ choose } x = −2. \;\; \dfrac{2(−2) − 3}{−2 − 1} = \dfrac{−7}{−3} = \dfrac{7}{3} ≥ 0 \\ &\text{Replacing \(-2\)pour\(x\) obtenir une réponse supérieure à\(\dfrac{7}{3}\)\(0\), ne comblant pas l'inégalité donnée dans le problème.} \ \ & \ text {Cette région\(x < −1\) est exclue de l'ensemble de solutions.} \ \ [0,25 pouce] & \ text {Pour} −1 < x < 1,5, \ text {choose} x = 0. \ ; \ ; \ dfrac {2 (0) − 3} {0 − 1} = \ dfrac {−3} {−1} = 3 ≥ 0 \ \ & \ text {Remplacer\(0\) pour des\(x\) résultats dans la réponse\(3\), qui est supérieure ou égale à\(0\), ce qui n'est pas ce que demande le problème.} \ \ & \ text {Cette région\(−1 < x < 1.5\) est exclue de l'ensemble de solutions.} \ \ [0,25 pouce] & \ text {Pour } x > 1, \ text {choose} x = 2. \ ; \ ; \ dfrac {2 (2) − 3} {2 − 1} = \ dfrac {1} {1} = 1 ≥ 0 \ \ & \ text {Remplacer\(2\) pour\(x\) résultats dans la réponse\(1\), qui est supérieure ou égale à\(0\). Cette région\(x > 1\) est exclue du jeu de solutions.} \ \ [0,25 pouce] &1/3 \ \ & \ text {Ce problème n'a pas de solution. \(\dfrac{2x − 3}{x + 1}\)ne sera jamais inférieur ou égal à\(0\).} \ end {tableau} \)
- \(\begin{array} &&\dfrac{x + 2}{x − 2} ≥ 0 &\text{Example problem} \\ &\dfrac{x + 2}{x − 2} ≥ 0 &\text{The quotient must be greater than or equal to \(0\).} \ \ &x + 2 = 0, \ ; \ ; x = −2 & \ text {Trouve les zéros du numérateur} \ \ &x − 2 = 0, \ ; \ ; x = 2 & \ text {Trouve les zéros du dénominateur} \ end {array} \)
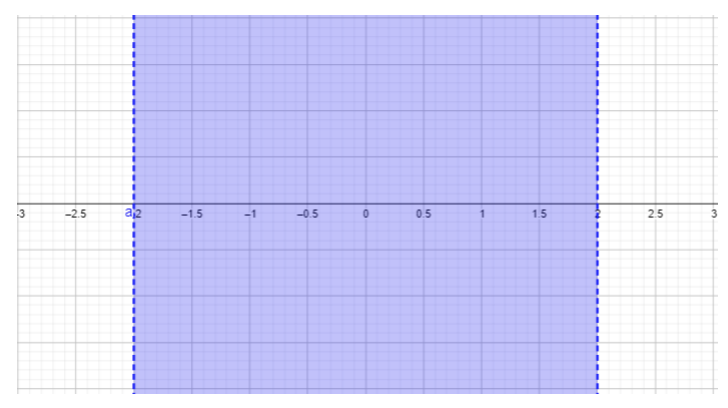
\(\begin{array} &&\text{For } x < −2, \text{ choose } x = −3. \dfrac{−3 + 2}{−3 − 2} = \dfrac{−1}{−5} = \dfrac{1}{5} ≥ 0 \\ &\text{Replacing \(-3\)pour les\(x\) résultats de la réponse\(\dfrac{1}{5}\), qui est supérieur ou égal à\(0\). Cette région\(x < −2\) est incluse dans l'ensemble de solutions.} \ \ [0,25 pouces] & \ text {Pour} −2 < x < 2, \ text {choose} x = 0. \ ; \ ; \ dfrac {0 + 2} {0 − 2} = \ dfrac {2} {−2} = −1 < 0 \ \ & \ text {Remplacer\(0\) pour\(x\) obtenir des résultats dans la réponse\(-1\), qui est inférieure à\(0\), non satisfaisante l'inégalité donnée dans le problème.} \ \ & \ text {Cette région n'\(−2 < x < 2\)est pas incluse dans l'ensemble de solutions.} \ \ [0,25 in] & \ text {Pour} x > 2, \ text {choose} x = 3. \ ; \ ; \ dfrac {3 + 2} {3 − 2} = \ dfrac {5} {1} = 5 ≥ 0 \ \ & \ text {Remplacer\(3\) pour les\(x\) résultats dans le réponse\(5\), qui est supérieur ou égal à\(0\). Cette région\(x > 2\) est incluse dans l'ensemble de solutions.} \ \ [0,25 pouce] & (−∞, −2) (2, ∞) \ \ & \ text {Réponse finale écrite en notation par intervalles (voir la section sur la notation par intervalles pour plus de détails).} \ end {tableau} \)
- \(\dfrac{x + 3}{x − 2} ≥ 0\)
- \(\dfrac{x − 2}{x − 1} ≤ 0\)
- \(\dfrac{2x − 1}{x + 2} ≤ 0\)
- \(\dfrac{2x − 3}{x + 1} ≥ 0\)


