7.6 : Exemples appliqués
- Page ID
- 165678
Pour mieux comprendre les concepts appris dans ce chapitre, appliquez-les à des situations réelles et à des problèmes quotidiens.
Les ventes totales de housses de téléphone dans un magasin de téléphonie populaire (en milliers) sont présentées dans la figure ci-dessous. Le mois de mars\(2016\), correspond à\(x = 0\).
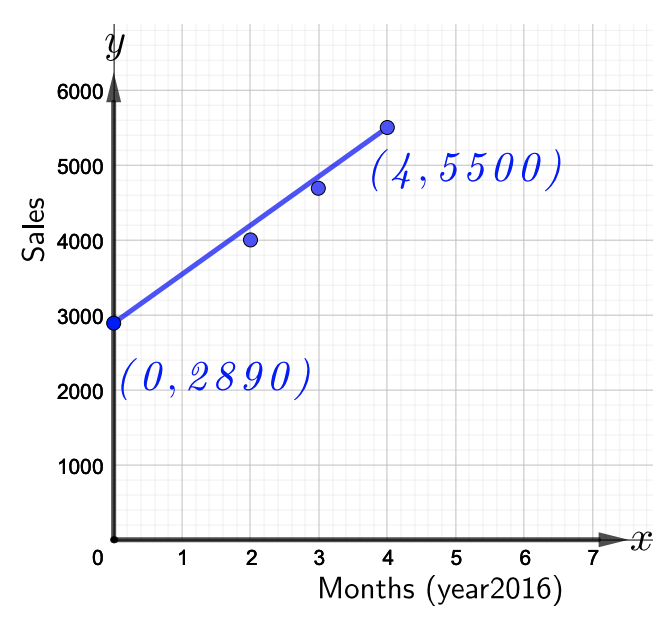
- Reportez-vous à la figure ci-dessus pour écrire une équation de la droite qui modélise les données. Qu'indique la pente ?
- Utilisez l'équation de la partie a pour estimer les ventes de housses de téléphone au mois de novembre,\(2016\).
Solution
- En vous référant à la figure ci-dessus, remarquez qu'il y a deux points,\((0, 2890)\) et\((4, 5500)\), qui se trouvent sur la ligne donnée. Utilisez les deux points pour trouver d'abord la pente. Ainsi,
\(m = \dfrac{5500 − 2890}{4 − 0} = \dfrac{2610}{4} = 652.5\)
Ainsi, la pente est\(652.5\). La pente étant positive, elle indique une augmentation. La pente indique donc que les ventes de housses de téléphone ont augmenté d'environ\($652.5\) par mois de mars\(2016\) à juillet\(2016\).
Utilisez la pente et l'\(y\)intersection\((0, 2890)\) pour écrire l'équation de la droite sous forme d'intersection de pente comme suit,
\(\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &y = 652.5x + 2890 &\text{Substituting \(m = 652.5\)et\(b = 2890\)} \ end {array} \)
- Maintenant, on indique que cela\(x = 0\) correspond au mois de mars et le problème demande d'approximer les ventes de housses de téléphone au mois de novembre\(2016\). \(x = 8\)Correspond donc au mois de novembre\(2016\). Substituer\(x = 8\) dans l'équation de la partie a. Ainsi,
\(\begin{array} &&y = 652.5x + 22980 &\text{Equation of the line from part a} \\ &= 652.5(8) + 2890 &\text{Substitute \(x = 8\)} \ \ &= 8110 & \ text {Multipliez puis ajoutez pour simplifier} \ end {array} \)
Par conséquent, les ventes de housses de téléphone au mois de novembre\(2016\) étaient d'environ\($8,110\).
Une mère s'inquiétait de savoir si son tout-petit consommait suffisamment de calcium. Le principal apport en calcium du tout-petit était sous forme de lait. La mère a enregistré les données pendant neuf mois afin de surveiller la consommation de lait du tout-petit. Les données sont représentées dans un diagramme dispersé qui montre la quantité de lait que le tout-petit a consommée chaque mois pendant neuf mois, de février à octobre, comme le montre la figure ci-dessous.
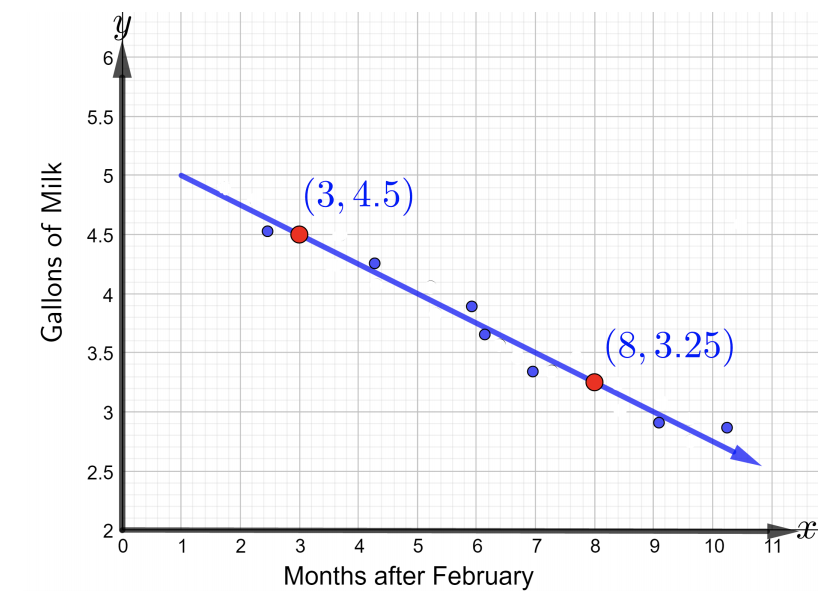
- Reportez-vous à la figure ci-dessus pour écrire une équation de la droite afin de modéliser les données données à l'aide des deux points étiquetés. Écrivez l'équation sous la forme d'une pente d'interception. Que peut-on dire à propos de la pente ?
- Utilisez l'équation de la droite trouvée dans la partie a pour prédire la quantité de substances douces que le tout-petit consommera en décembre.
Solution
- Pour écrire l'équation de la droite, trouvez d'abord la pente à l'aide des deux points étiquetés,\((3, 4.5)\) et\((8, 3.25)\). Ainsi,
\(m = \dfrac{3.25 − 4.5}{8 − 3} = −\dfrac{1.25}{5} = −0.25\)
La pente est négative signifie que la consommation de lait du tout-petit diminue d'environ\(0.25\) gallons de lait par mois.
Comme le\(y\) paramètre -intercept n'est pas indiqué, il ne sera pas possible d'utiliser la forme d'interception de pente. Utilisez plutôt la pente et l'un des deux points étiquetés dans le formulaire de pente ponctuelle pour trouver l'équation de la droite. Ainsi,
\(\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ &y − 4.5 = −0.25(x − 3) &\text{Substitute \(m = −0.25\)et pointez\((3, 4.5)\) avec\(x_1 = 3\) et\(y_1 = 4.5\)} \ \ &y−4.5 = −0,25x+0,75 & \ text {Répartir\(-0.25\) entre les deux termes de droite} \ \ &y = −0,25x + 5,25 & \ text {Ajoutez\(4.5\) des deux côtés de l'égalité pour résoudre\(y\) et obtenir l'équation sous la forme Slope-Intercept } \ end {tableau} \)
\(y = −0.25x + 5.25\)Il s'agit donc de l'équation de la droite qui représente les données données dans la figure ci-dessus et qui se présente sous forme d'intersection de pente.
- Pour prédire combien de gallons de lait le tout-petit consommera en décembre, trouvez d'abord\(x\) qui correspond au mois de décembre. Il est donné qui\(x = 0\) correspond au mois de février. À partir du mois de mars avec\(x = 1\),\(x = 10\) correspond au mois de décembre. Substituez\(x = 10\) dans l'équation la droite trouvée dans la partie a et résolvez\(y\) comme suit,
\(\begin{array} &&y = −0.25x + 5.25 &\text{Equation of the line found in part a} \\ &= −0.25(10) + 5.25 &\text{Substitute \(x = 10\)} \ \ &= −2,5 + 5,25 & \ text {Multipliez puis ajoutez pour simplifier} \ \ &= 2,75 & \ end {array} \)
Par conséquent, le tout-petit consommera environ des\(2.75\) gallons de lait en décembre.
Les ventes annuelles d'un certain modèle d'imprimantes dans un célèbre magasin d'électronique sont indiquées dans la figure ci-dessous, où\(2012\) correspond l'année\(x = 0\).
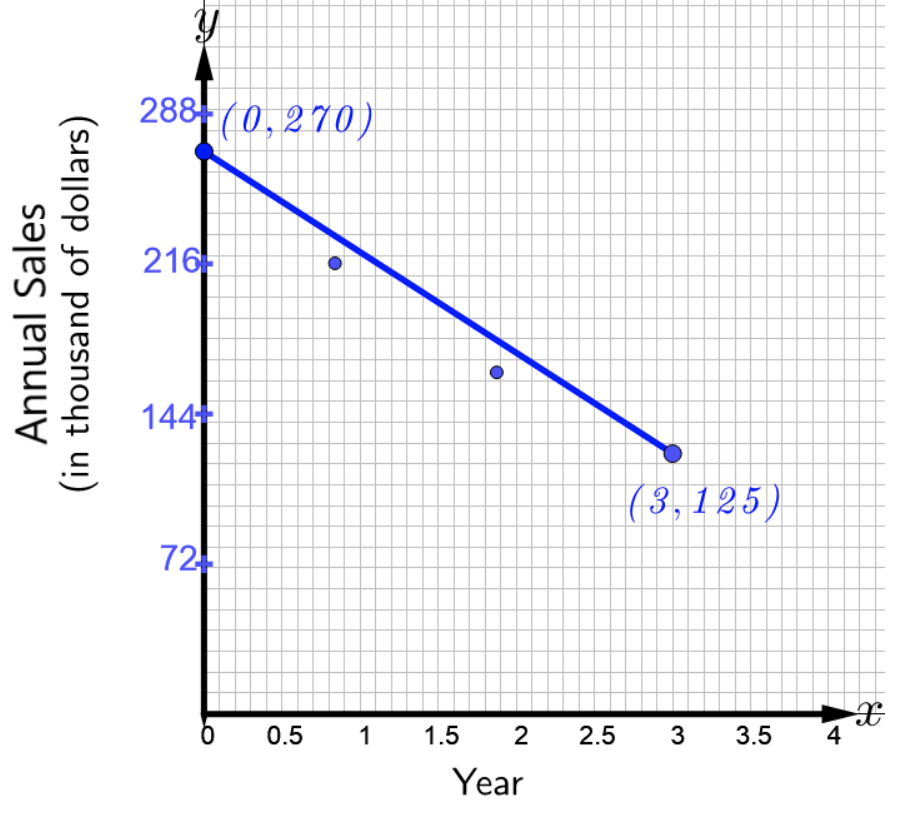
- Reportez-vous à la figure ci-dessus pour écrire une équation de la droite qui modélise les données. Qu'indique la pente ?
- Utilisez l'équation de la ligne figurant dans la partie a pour obtenir une estimation des ventes des imprimantes au cours de l'année\(2016\).
John a acheté un cornet de crème glacée de\(11.2\) cm de haut. Il faisait très chaud, la glace a commencé à fondre à une vitesse de\(2\) cm par minute. John s'est intéressé à la vitesse à laquelle sa glace fondait et a voulu savoir quelle quantité de glace il resterait au bout de\(2.5\) quelques minutes.
- Trouvez une équation de la droite qui modélise les données sous forme d'intersection de pente.
- Déterminez la quantité de crème glacée qui reste après\(2.5\) quelques minutes.


