Skip to main content
Global

3,4 : (a, b)

  1. Last updated
  2. Save as PDF
  • Page ID
    165655

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Dans cette section, les deux points de terminaison ne sont pas inclus dans l'intervalle.

    Exemple Template:index

    \((2,5)\)

    Solution
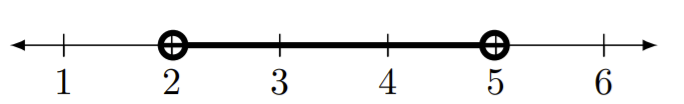
    clipboard_ed02584abc419d9b4c552a7f3a0665800.png
    Figure Template:index

    L'intervalle ci-dessus inclut tous les nombres compris entre 2 et 5, mais comme l'intervalle comporte des parenthèses sur les côtés gauche et droit de l'intervalle, les points finaux ne sont pas inclus.

    Exemple Template:index

    \((-4,10)\)

    Solution
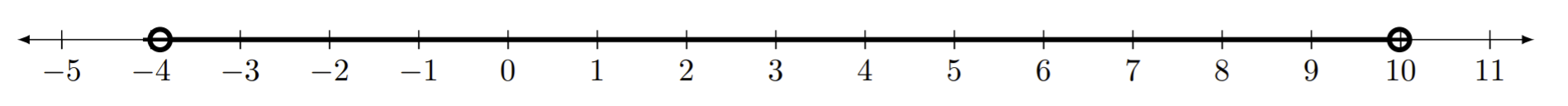
    clipboard_e3c08ff2a1c09de1cdd8d5fd910f40778.png
    Figure Template:Index

    Comme pour l'explication des exemples précédents, les points de fin ne sont pas inclus dans l'intervalle. L'intervalle inclut donc tous les nombres compris entre -4 et 10, mais pas -4 et 10.

    À l'heure actuelle, les élèves devraient avoir une idée précise des chiffres inclus et non inclus dans les exemples ci-dessus. Les élèves devraient également être capables d'analyser n'importe quelle ligne numérique et d'écrire la notation d'intervalle appropriée pour cette ligne numérique. Essayez les exercices suivants pour vérifier votre compréhension.

    Exercice Template:index

    Tracez une ligne numérique pour les intervalles suivants et listez au moins trois nombres à l'intérieur de l'ensemble.

    1. \((0,1)\)
    2. \((-11,-5)\)
    3. \((100,325)\)
    4. \((5,6)\)
    5. \((12.1, 26.55]\)
    Exercice Template:index

    Tracez une ligne numérique qui correspond aux intervalles suivants.

    1. \([-2,3)\)
    2. \([-5,-2]\)
    3. \((0,5]\)
    4. \((-3,4)\)
    5. \([-3,-2]\)
    6. \((-7,2.5)\)
    Exercice Template:index

    Écrivez la notation d'intervalle appropriée pour les lignes numériques données.

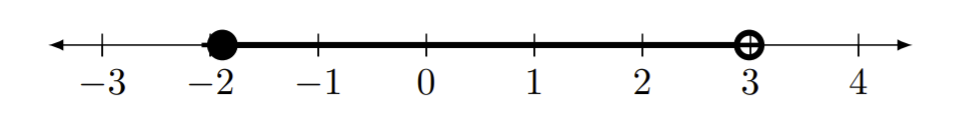
    1. clipboard_eaf25f54bdd51292793561ac52327ea79.png
      Figure Template:Index
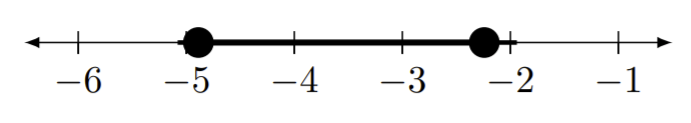
    2. clipboard_ea30f5db1fcf59dc703453b44b6e594b1.png
      Figure Template:Index
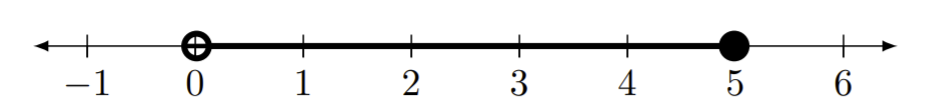
    3. clipboard_e94592852e95353bec73409c17b019348.png
      Figure Template:Index
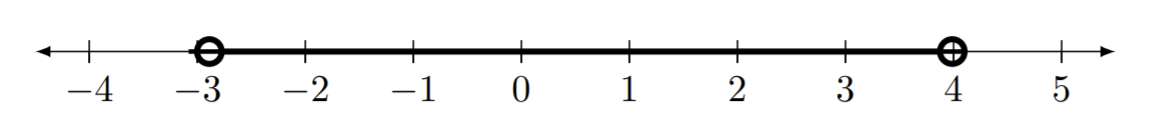
    4. clipboard_e8a9241fcff6d38e501a451cb77c26cf9.png
      Figure Template:Index
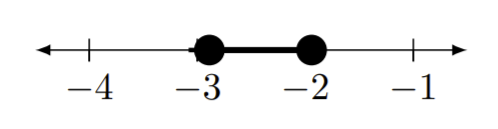
    5. clipboard_e18c65da53a6f43b9ae17c6c57e84faa8.png
      Figure Template:Index
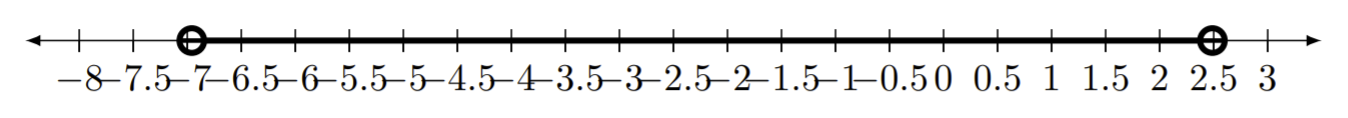
    6. clipboard_e65e3add979e445d287ea5138a0be4c46.png
      Figure Template:Index