Skip to main content
Global

3,3 : (a, b)

  1. Last updated
  2. Save as PDF
  • Page ID
    165649

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Faites attention à la façon dont la notation par intervalles est écrite ! La notation de cette section ressemble à celle de la section précédente, mais elle n'est pas la même. En regardant la notation de plus près, il devient clair que l'extrémité de gauche n'est pas incluse dans l'ensemble alors que l'extrémité de droite est incluse dans l'intervalle.

    Exemple Template:index

    \((2,5]\)

    Solution
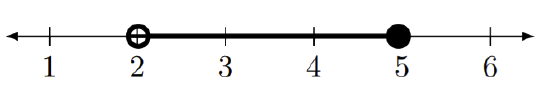
    clipboard_e82f3d9ad7e52b90b6c3485eb9f2a34c4.png
    Figure Template:index

    L'extrémité gauche, qui correspond au numéro 2, ne se trouve pas sur l'intervalle. Le bon point de terminaison, qui correspond au numéro 5, est inclus. Des exemples de nombres dans cet ensemble sont 3, 4, 4,5 et 5

    Exemple Template:index

    \((-4,10]\)

    Solution
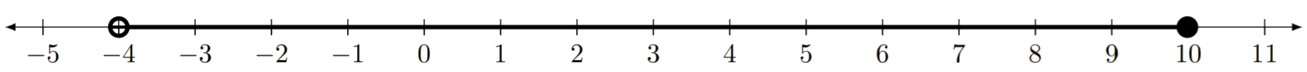
    clipboard_edee56f85a930d8c01b519a3386d4917b.png
    Figure Template:Index

    Les extrémités de cet intervalle se comportent de la même manière que dans l'exemple 1. Lorsque vous créez un graphique, n'oubliez pas de placer le point de terminaison\(\bullet\)\(\circ\) lorsque le point de terminaison est inclus et celui où le point Quelques exemples de nombres compris dans cet intervalle sont -3,99, -2, 0 et 10.

    Exercice Template:index

    Tracez une ligne numérique pour les intervalles suivants et listez au moins trois nombres à l'intérieur de l'ensemble.

    1. \((6,12]\)
    2. \((-31,-20]\)
    3. \((-200,-199]\)
    4. \(\left(\dfrac{3 }{4} ,5 \right] \)
    5. \(\left(\dfrac{−11 }{2} , \dfrac{7 }{2} \right]\)
    6. \((0.15, 6.95]\)