Skip to main content
Global

2.1 : Quadrants de définition et d'étiquetage

  1. Last updated
  2. Save as PDF
  • Page ID
    165742

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Définition : Système de coordonnées rectangulaires

    Le système de coordonnées rectangulaires, également connu sous le nom de système de coordonnées cartésiennes, est basé sur une grille et formé de deux lignes numériques perpendiculaires, la ligne numérique horizontale appelée axe x et la ligne numérique verticale appelée axe y. Chaque point du système de coordonnées rectangulaires peut être identifié par des coordonnées x et y uniques.

    Les deux lignes numériques perpendiculaires se croisent au point\((0, 0)\) et sont appelées origine. Le système de coordonnées rectangulaires est divisé en quatre régions. Les régions sont appelées quadrants et étiquetées en chiffres romains comme suit : quadrant I, quadrant II, quadrant III et quadrant IV, comme le montre la figure ci-dessous

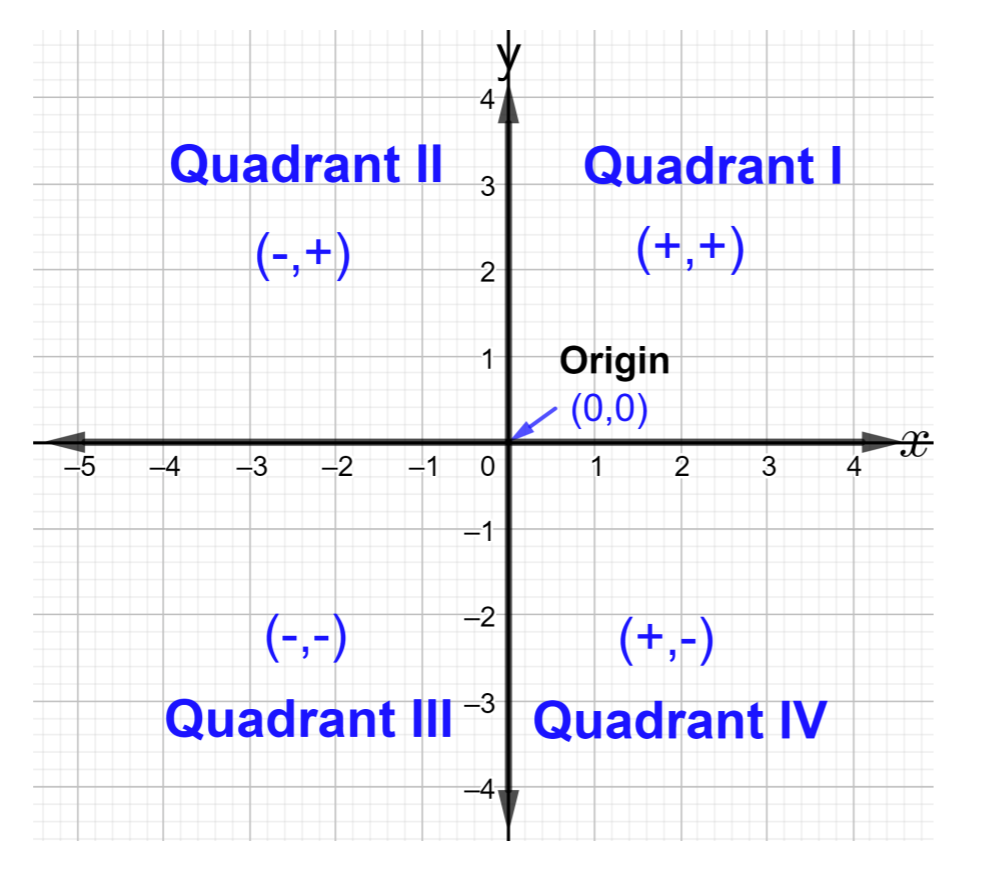
    clipboard_eda24e99442f9af06866b6dd2ced5217d.png
    Figure Template:index

    Chaque point du plan de coordonnées correspond à une paire ordonnée unique\((x, y)\), où\(x\) et\(y\) sont des nombres réels. La paire ordonnée a toujours la coordonnée X en premier (à gauche) et la\(y\) seconde (à droite). \((6, 4)\),\(\left(−.33, \dfrac{1}{5} \right)\)\((100, −2)\),\(\left( \sqrt{ 3}, \dfrac{1 }{2}\right )\) sont quelques exemples de paires ordonnées. Lisez la paire ordonnée\((6, 4)\) comme « le point six, quatre » où 6 est la\(x\) coordonnée et 4 est la\(y\) coordonnée.

    Exercice Template:index
    1. Comment s'appellent les points qui ont la forme\((x, y)\) ?
    2. Identifiez les coordonnées des paires ordonnées suivantes :\((−10, 0)\),\((0.5, −6)\),\(\left(\dfrac{1}{ 2} , −\dfrac{ 5 }{3} \right)\)
    3. Nommez et indiquez la paire ordonnée du point d'intersection des axes perpendiculaires du système de coordonnées rectangulaires.
    4. Indiquez les 4 régions dans le système de coordonnées rectangulaires.
    5. Nommez la première coordonnée d'une paire ordonnée.
    6. Nommez la deuxième coordonnée d'une paire ordonnée.
    7. Qu'est-ce que la ligne numérique horizontale dans le système de coordonnées rectangulaires ?
    8. Qu'est-ce que la ligne numérique verticale dans le système de coordonnées rectangulaires ?