4.12 : Exemples de fonctions appliquées
- Page ID
- 165799
Exemples appliqués de fonctions (alias problèmes de mots !) peuvent prendre de nombreuses formes.
Préparez-vous à utiliser tout type de fonction examiné dans ce chapitre.
Un emploi d'été paie du temps et demi pour les heures supplémentaires si un travailleur travaille plus de 40 heures. Après 40 heures, le travailleur est rémunéré 1,5 fois le\($12.00\) taux horaire.
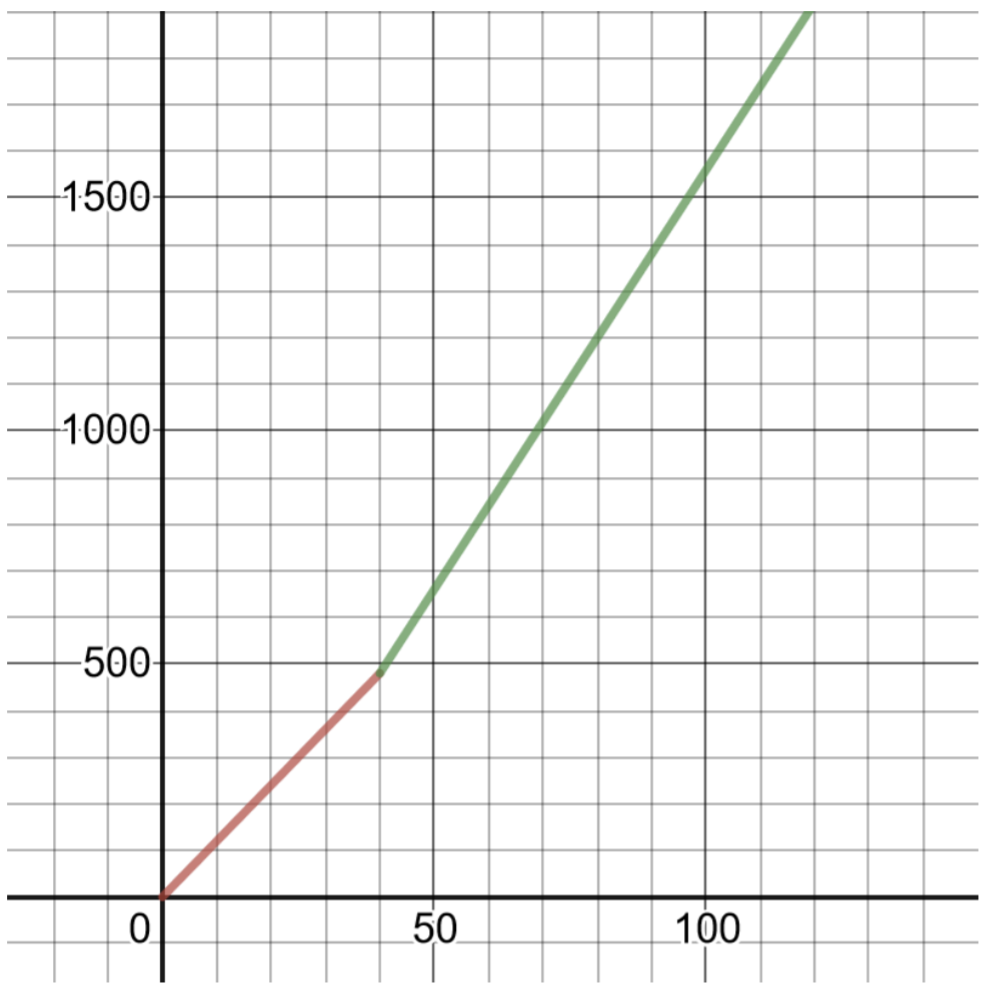
- Écrivez et représentez graphiquement une fonction par morceaux qui donne le salaire hebdomadaire P en termes de nombre d'heures travaillées h. CONSEIL : Cela peut être délicat, réfléchissez à la façon d'exprimer le nombre d'heures au-dessus de 40.
- Combien seront gagnés en travaillant 45 heures ?
Solution
- Pour écrire la fonction par morceaux :
\(P (h) = \left\{\begin{array}{cc} 12h &0 < h \leq 40 \\ 12(40) + 1.5(12)(h − 40) &h > 40\end{array} \right.\)
Pour représenter graphiquement cette fonction, créez un tableau des solutions :
|
Tableau des solutions pour\(P (h) = 12h \) Domaine\(0 < h \leq 40\) |
|
| \(h\) | \(P(h)\) |
| 1 | \($12.00\) |
| 10 | \($120.00\) |
| 40 | \($480.00\) |
|
Tableau des solutions pour\(P (h) = 12(40) + 1.5(7)(h − 40) \) simplifié\(P (h) = 18h − 240 \) Domaine\(h > 40\) |
|
| \(h\) | \(P(h)\) |
| 41 | 498 |
| 45 | 570 |
| 50 | 660 |
| 60 | 840 |
- \($570.00\)pour 45 heures de travail (voir Tableau des solutions)
La NASA lance une fusée en\(t=0\) quelques secondes. Sa hauteur, en mètres au-dessus du niveau de la mer, en fonction du temps est donnée par\(h(t) = −4.9t^2 + 46t + 227\).
- En supposant que la fusée s'écrasera dans l'océan, à quelle heure se produiront les éclaboussures ?
- À quelle hauteur au-dessus du niveau de la mer la fusée atteint-elle son apogée ?
Solution
- Au démarrage\(h(t) = 0\), définissez la fonction sur 0 et résolvez pour\(t\).
\(0 = −4.9t 2 + 46t + 227\)
Utilisez la formule quadratique pour résoudre cette équation, avec\(a = −4.9\),\(b = 46\),\(c = 227\)
\(\begin{aligned} t &= \dfrac{−46 \pm \sqrt{46^2 − 4(−4.9)(227) }}{2(−4.9) } && \text{Quadratic Formula} \\ t &= \dfrac{−46 \pm \sqrt{ 2116 + 4449.2 }}{−9.8 } &&\text{Simplify the radical} \\ t &= \dfrac{46 \pm \sqrt{ 6565.2 }}{9.8 } &&\text{Further simplify the radical, divide all terms by -1 (still have } \pm\text{ )} \\t &= \dfrac{46 \pm 81.026 }{9.8 } &&\text{Square root} \\ t &= \dfrac{46 + 81.026 }{9.8 } &&\text{Addition} \\ t &= \dfrac{46 − 81.026 }{9.8} && \text{Subtraction} \\ t& = 12.96 \text{ and } t = −3.57&& \text{Two solutions, reject negative solution because time cannot be negative} \\ t &= 12.96 \text{ seconds }&&\text{Final Answer} \end{aligned}\)
- À quelle hauteur au-dessus du niveau de la mer la fusée atteint-elle son apogée ?
Le signe du coefficient du terme principal de la fonction quadratique\(h(t) = −4.9t^2 + 46t + 227\) indique dans quelle direction s'ouvre la parabole. Le coefficient est\(−4.9\), et comme il est négatif, la fonction quadratique s'ouvre vers le bas.
Nous devons maintenant trouver le sommet. La valeur y de la paire ordonnée de sommets indiquera où commence la plage.
Le sommet est\(\left(− \dfrac{b }{2a} , f\left( −\dfrac{ b }{2a}\right) \right)\), avec\(a = −4.9\) et\(b = 46\)
Le sommet est\(\left(−\dfrac{ 46 }{2(−4.9) }, f\left( − \dfrac{46 }{2(−4.9)}\right)\right)\)
Le sommet est\((4.694, f (4.694))\) qui est\((4.694, (−4.9)(4.694)^2 + (46)(4.694) + 227 ))\) ou\((4.694, 334.959)\)
La hauteur de la fusée à son apogée est de\(334.959\) mètres au-dessus du niveau de la mer.
Pour promouvoir les ventes de groupe pour une croisière en Alaska, une agence de voyages réduit le prix normal du billet de\($4500\) par\($5\) pour chaque personne du groupe.
- Écrivez une équation linéaire qui donne le coût par personne\(f(p)\), si\(p\) les personnes voyagent en groupe.
- Utilisez l'équation pour déterminer le coût pour 50 personnes.
Solution
- Comme le coût par personne est réduit du même montant pour chaque personne, il s'agit d'une équation linéaire.
\(f(x) = mx + b\)Utilisez-le, ou écrions-le ainsi\(f(p) = mp + b\), avec\(f(p)\) le coût par personne.
\(f(p) = mp + b\)
Comme le coût par personne est réduit de 5$ pour chaque personne du groupe, c'est la pente de la ligne.
\(\begin{aligned} f(p)&= −5p + b && \text{Slope-intercept form of the equation of a line} \\ f(p) &= −5p + 4500 &&\text{The y-intercept is the starting point, so the regular ticket price of }$4500 {is the y-intercept} \\ f(p)& = −5p + 4500 && \text{Linear Equation} \end{aligned}\)
- Utilisez l'équation pour déterminer le coût pour 50 personnes.
\(\begin{aligned} f(50) &= −5(50) + 4500 && \text{Replace p with 50 people in the Linear Equation} \\ f(50) &= −250 + 4500 &&\text{Simplify} \\ f(50) &= 4250 &&\text{Simplify} \\ \text{If }50 &\text{ people take the cruise, the cost per-person for the cruise is } $4250&&\text{Final Answer }\end{aligned}\)
Résolvez les problèmes de fonction appliqués suivants :
- Un tailleur facture des frais de base de\($20\) plus\($5\) par lettre pour coudre le nom d'un athlète au dos d'une veste.
- Écrivez une équation linéaire qui déterminera le coût d'un nom contenant x lettres cousues au dos d'une veste.
- Quel est le coût d'un nom composé de 11 lettres ?
- À Acapulco, au Mexique, une attraction touristique populaire est de regarder des hommes plonger d'une falaise jusqu'à l'eau à 75 pieds plus bas. La hauteur d'un plongeur\(f(t)\) au-dessus de l'eau (en pieds),\(t\) quelques secondes après la plongée, est donnée par\(f(t) = −16t^2+75\).
- Combien de temps dure une plongée ?
- Dans un certain pays, l'impôt sur le revenu est calculé comme suit : Il n'y a pas d'impôt sur le revenu jusqu'à\($15000\). Les revenus\($15000\) supplémentaires et\($30000\) inférieurs sont imposés à\(12%\). Les revenus\($30000\) excédentaires sont imposés à\(18%\).
- Écrivez la fonction par morceaux des informations ci-dessus et esquissez son graphique.
- Déterminez le montant de l'impôt à payer sur un revenu de\($18000\).


