Skip to main content
Global

3.5: تدوين الفاصل الزمني وما لا نهاية

  1. Last updated
  2. Save as PDF
  • Page ID
    166895

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    ما هي اللانهاية؟ إنفينيتي ليست رقمًا حقيقيًا. إنفينيتي أكبر من أي رقم يمكن تخيله. إنها فكرة عدم وجود حدود. الخط هو مثال على عدم وجود حدود. على سبيل المثال، يحتوي خط الأعداد على أسهم في النهاية لتمثيل فكرة عدم وجود حدود. الرمز المستخدم لتمثيل اللانهاية هو\(\infty\). على الجانب الأيسر من خط الأعداد يوجد\(−\infty\) وعلى الجانب الأيمن من خط الأعداد\(\infty\) وصف السلوك اللامحدود لخط الأعداد.

    تدوين الفاصل الزمني خط الأرقام
    أ)\((12,\infty)\)
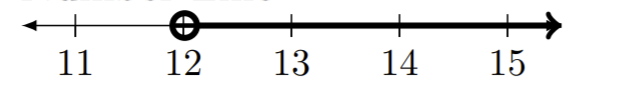
    clipboard_e80433e1e62fd9286767d7fccd338cf9b.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/03:_الترميز_الفاصل_الزمني/3.05:_تدوين_الفاصل_الزمني_وما_لا_نهاية), /content/body/table/tbody/tr[2]/td[2]/figure/figcaption/span, line 1, column 17
    ب)\([-5,\infty)\)
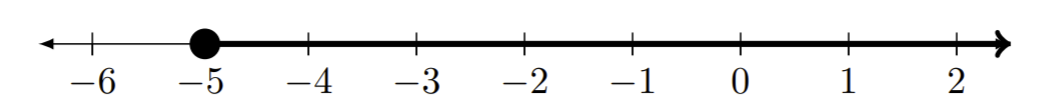
    clipboard_eb315c734eff17646d4b6150afe365542.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/03:_الترميز_الفاصل_الزمني/3.05:_تدوين_الفاصل_الزمني_وما_لا_نهاية), /content/body/table/tbody/tr[3]/td[2]/figure/figcaption/span, line 1, column 17
    ج)\((−\infty,4)\)
    clipboard_e347ccb8b609ce4a6a16613afe5ef2c4b.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/03:_الترميز_الفاصل_الزمني/3.05:_تدوين_الفاصل_الزمني_وما_لا_نهاية), /content/body/table/tbody/tr[4]/td[2]/figure/figcaption/span, line 1, column 17
    د)\((−\infty,0]\)
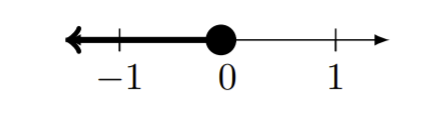
    clipboard_e960bf6751735e85b398571075c5f0bf9.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/03:_الترميز_الفاصل_الزمني/3.05:_تدوين_الفاصل_الزمني_وما_لا_نهاية), /content/body/table/tbody/tr[5]/td[2]/figure/figcaption/span, line 1, column 17
    ه)\((−\infty,\infty)\)
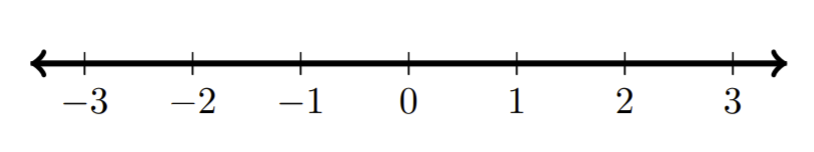
    clipboard_e65f0217f121cc70ff0562beb8ad1573f.png
    الشكل
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/03:_الترميز_الفاصل_الزمني/3.05:_تدوين_الفاصل_الزمني_وما_لا_نهاية), /content/body/table/tbody/tr[6]/td[2]/figure/figcaption/span, line 1, column 17

    ملاحظة: نظرًا لأنه\(\infty\) ليس رقمًا حقيقيًا، فمن الضروري استخدام الأقواس (،). \(\infty\)لا يمكن تضمينها في الفاصل الزمني.

    التمرين
    ParseError: invalid ArgList (click for details)
    Callstack:
    at (اللغة_العربية/(__)/03:_الترميز_الفاصل_الزمني/3.05:_تدوين_الفاصل_الزمني_وما_لا_نهاية), /content/body/section/header/div/h5/span/span, line 1, column 17

    ارسم خط أرقام يتوافق مع الفواصل الزمنية التالية.

    1. \((−\infty,5)\)
    2. \([-5,\infty)\)
    3. \((−\infty,\infty)\)
    4. \((-3,\infty)\)
    5. \((−\infty,-2]\)